TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ PİSAGOR TEOREMİ
TEOREMLER VE İSPATLAR
PİSAGOR TEOREMİ
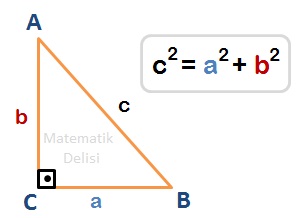
📚 Bir dik üçgende dik açının karşısındaki kenarın karesi, diğer iki kenarın kareleri toplamına eşittir.
İSPAT
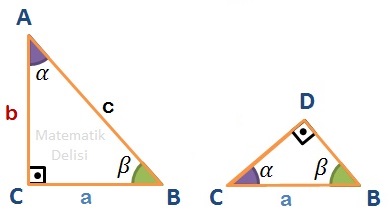
Pisagor teoremini ispatlamak için dik açının olduğu köşeden hipotenüse dik bir doğru parçası çizip, üçgenlerde benzerliği kullanıyoruz.
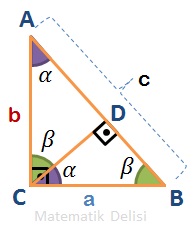
Hipotenüse karşı köşeden bir dik indirdiğimizde, ... açısının ... açısına eşit olduğunu görebiliriz. Bu açıya ... diyelim. ...'yı 90⁰'ye tamamlayan ... açısına da ... ismini verelim.
Hipotenüse dik indirdiğimizde, 3 farklı üçgen tanımlayabiliriz: ..., ... ve ...
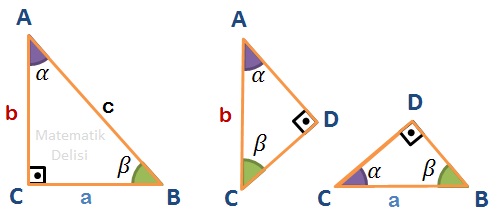
Bu 3 üçgenin de birer açısının 90⁰'ye, birer açısının ise ...'ya eşit olduğunu görüyoruz. Buna göre üçgenlerin iç açılarının eşit olduğunu söyleyebiliriz. Buradan ..., ... ve ... üçgenlerinin benzer oldukları çıkarımını yapabiliriz.
... ... ...
Benzer üçgenlerin kenar uzunluklarının oranları aynıdır. Bu özelliği kullanarak, |AB| uzunluğunu veya ...'yi ... ve ... cinsinden bulacağız. ...'nin uzunluğu AD ve DB doğru parçalarının uzunlukları toplamına eşittir.
... = |AD|+|DB| (1)
Şimdi sırayla |AD| ve |DB|'yi ..., ... ve ... cinsinden bulalım.
|AD|'nin uzunluğu
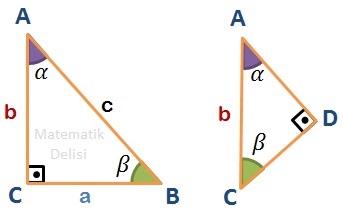
... üçgeninde dik açının karşısında ... varken, ... üçgeninde ... vardır. Dolayısıyla, ... ve ... üçgenleri arasındaki benzerlik oranı ...'dir. ... üçgeninde ... açısının karşısında ... olduğuna göre, ... üçgeninde bu açının karşısında ... olmalıdır ve bu uzunluk |AD|'ye eşittir.
|AD| = ... (2)
|DB|'nin uzunluğu
... üçgeninde dik açının karşısında ... ve ... üçgeninde aynı açının karşısında ... bulunmaktadır. Buna göre, bu üçgenlerin benzerlik oranı ...'dir. ... üçgeninde ... açısının karşısında ... olduğu için ... üçgeninde aynı açının karşısında ... bulunmalıdır. ... üçgeninde ... açısının karşısındaki uzunluk |DB|'ye eşittir.
|DB| = ... (3)
(2) ve (3)'teki uzunlukları (1)'de yerlerine yazarsak,
...
olduğunu buluruz. Bu eşitliğin her iki tarafını da ... ile çarptığımızda ... eşitliğini elde ederiz.
TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ PİSAGOR TEOREMİ