TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ KENARORTAYLARIN KESİŞİMİ
TEOREMLER VE İSPATLAR
ÜÇGENDE KENARORTAYLAR NEDEN BİR NOKTADA KESİŞİRLER?
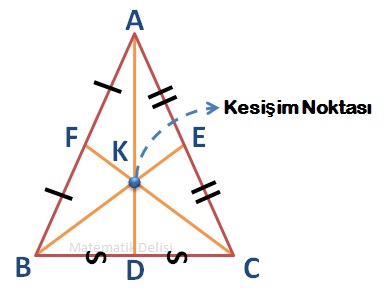
Bir üçgendeki tüm kenarortaylar bir noktada kesişirler.
İSPAT
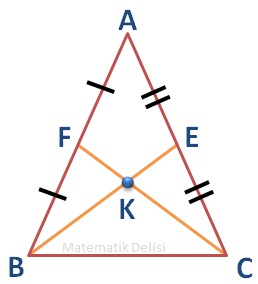
📚 Bir ... üçgeninde AB ve AC kenarlarına ait kenarortayları çizelim. Bu iki kenarortayın kesişim noktasına K ismini verelim.
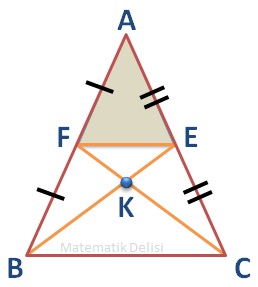
Şimdi E ve F noktalarını birleştirelim. ... ve ... üçgenlerinin
- hem tepe açıları
- hem de bu açıyı oluşturan kenarların oranları
eşit olduğu için bu üçgenler benzerdir.
... ... ...
Yukarıdaki benzerlik oranını tabanlara uyguladığımızda,
... ...
ilişkisini buluruz. |BC|'ye ... dersek, |FE| uzunluğu ...'ye eşit olur. Ayrıca, benzerlikten dolayı, ... ve ... açılarının eşit olduklarını görürüz. Bu da bize FE ve BC doğru parçalarının paralel olduklarını gösterir.
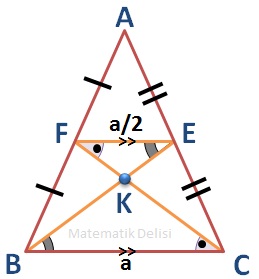
FE//BC olduğundan, iç ters açıları kullanarak
- ... ve
- ...
eşitliklerini bulabiliriz.
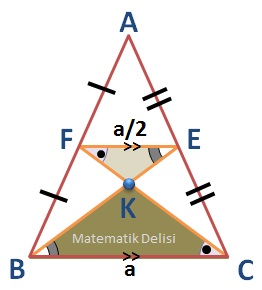
Bu eşitlikler, ... ve ... üçgenlerinin benzer olduklarını gösterir. benzerlik oranını |EK| ve |BK| kenarları için uyguladığımızda
... ... (1)
olduğunu buluruz. Başka bir değişle, K noktası, BE kenarortayını 2 parçaya böler. Bu parçalardan kenara yakın olan, diğerinin yarısı kadardır.
Şimdi de aynı işlemleri AC ve BC kenarlarına ait kenarortaylar için tekrar edelim.
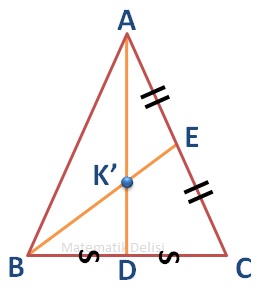
Halen üç kenarortayın aynı noktada kesiştiklerini ispatlamadığımız için AD ve BE'nin kesişme noktasına K'dan farklı bir isim verelim.
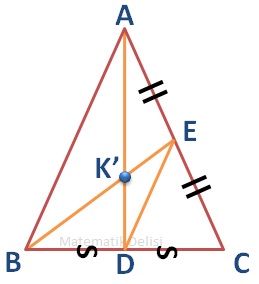
Daha önce yaptığımız gibi çizdiğimiz kenarortayların kenarlarla kesiştiği noktaları birleştirelim.
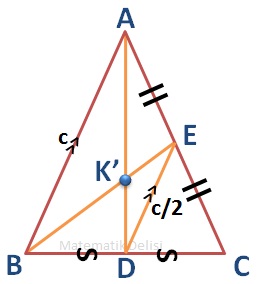
... ve ... üçgenlerinin benzerliğini kullanarak,
- ED//AB ve
- ... ...
olduğunu bulabiliriz. Bu defa da ... ve ... üçgenlerinin benzerliğini kullanıp, ispatın başındaki basamakları izleyerek
... ... (2)
olduğunu görebiliriz.
Farklı kenarortayların kesişimi için (1) ve (2)'yi incelediğimizde BE kenarortayının hem CF ile hem de AD ile kesişiminin aynı oranları verdiğinden, K ile K' noktalarının aynı nokta olması gerektiğini görürüz. Böylece, üç kenarortayın aynı noktada kesiştiği çıkarımını yapabiliriz.
TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ KENARORTAYLARIN KESİŞİMİ