BÖLÜM 2: ÜÇGENLERDE KENARORTAY

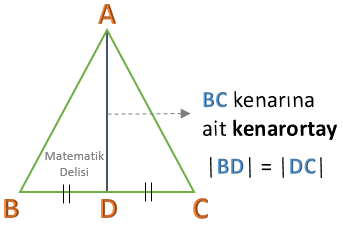
Üçgenin bir köşesinden karşı tarafındaki kenarın orta noktasına indirilen doğru parçasına kenarortay ismi verilir. Üçgende, her kenar için ayrı bir kenarortay çizilebilir. Bir kenarortay, ait olduğu kenarı iki eşit parçaya böler.

Her kenar için ayrı bir kenarortay tanımlanabildiği için bir üçgende üç kenarortay vardır.

ÖRNEK:

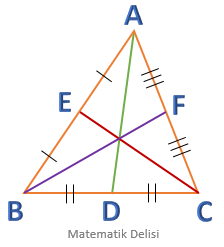
ABC üçgeninde,

BC kenarına ait kenarortay AD ile,
AB kenarına ait kenarortay CE ile ve
AC kenarına ait kenarortay BF ile

gösterilmiştir.

İki doğru parçasının aynı uzunluklukta olduğu, üzerlerine aynı işaret koyularak gösterilebilir. Örneğin, yukarıdaki üçgende,

|AE| = |EB| olduğunu göstermek için [AE] ve [EB] üzerine tek çizgi,
|BD| = |DC| olduğunu göstermek için [BD] ve [DC] üzerine çift çizgi, ve
|AF| = |FC| olduğunu göstermek için [AF] ve [FC] üzerine üç çizgi

konulmuştur.

KENARORTAYLARIN KESİŞİM NOKTASI

Bir üçgendeki kenarortaylar aynı noktada kesişir. (Nedenini öğrenmek için tıklayın.) Kenarortayların kesişim noktası her zaman üçgenin içindedir.

Kenarortayların kesişim noktası-dar açılı üçgen

Kenarortayların kesişim noktası-dik açılı üçgen

Kenarortayların kesişim noktası-geniş açılı üçgen

ÖRNEK:

Yukarıdaki şekilde [AD] doğru parçası ABC üçgeninin BC kenarına ve [AE] doğru parçası ADC üçgeninin DC kenarına ait kenarortaydır. |DE| = 2 cm ve ABC bir eşkenar üçgen olduğuna göre, ABC üçgeninin çevresi kaç santimetredir?

[AE] doğru parçası DC kenarını iki eşit parçaya böler.

|EC| = |DE| = 2 cm

Buna göre, |DC| uzunluğu 4 cm'dir.

|DC| = |DE| + |EC| = 2 + 2 = 4 cm

[AD] doğru parçası ise, BC kenarını iki eşit parçaya böler.

|BD| = |DC| = 4 cm

|BC| uzunluğu |BD| ve |DC| uzunluklarının toplamına eşittir.

|BC| = |BD| + |DC| = 4 + 4 = 8 cm

Bir kenar uzunluğu 8 cm olan ABC üçgeninin çevresi 3 × 8 = 24 cm'dir.

→KONU ANASAYFASINA DÖN←