İSPAT

ÜÇGENLER -Yükseklik, Kenarortay ve Açıortay konusunda öğrendiğimiz gibi, yüksekliklerin kesişme noktası, iç açılarına bağlı olarak, üçgenin içinde, üzerinde veya dışında olabilir. Yukarıdaki teoremi sırasıyla dar açılı, geniş açılı ve dik açılı üçgenler için ispatlıyoruz.

A) Dar açılı üçgenler

Dar açılı bir ... üçgeninde AB ve AC kenarlarına ait yükseklikleri çizelim. Bu iki doğru parçası üçgenin içerisinde H gibi bir noktasında kesişir. Daha sonra, A ve H noktalarından geçen ve BC kenarı ile kesişen bir AD doğru parçası çizelim. Eğer AD doğru parçası BC kenarı ile dik açı yapıyorsa (BC kenarının yüksekliği ise), tüm yüksekliklerin ortak bir H noktasında kesiştiklerini söyleyebiliriz. Bu nedenle dar açılı bir üçgende bu teoremin doğru olduğunu gösterebilmek için ... açısının 90⁰ olduğunu kanıtlamamız gerekir.

... ve ... açıları eşittir. Buna göre ... açısının dik açı olabilmesi için ... ve ... açılarının da eşit olması gerekir. Bu durum ise, ... ile ... üçgenlerinin benzer olmasını gerektirir. Bu nedenle, ispat için göstermemiz gereken şey, ... ve ... üçgenleri arasındaki benzerliktir.

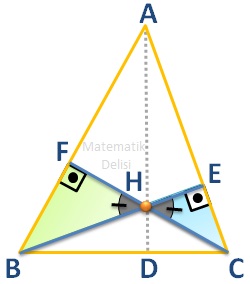
Önce ... ve ... üçgenlerini irdeleyelim. İki üçgen de dik üçgendir. Ayrıca, ... ve ... açıları eşittir. Buna göre, ... ve ... üçgenlerinin benzer olduklarını söyleyebiliriz.

... üçgenindeki |EH| uzunluğuna ... ve |EC| uzunluğuna ... diyelim. ... bir dik üçgen olduğundan |HC| uzunluğu ... olur. Eğer ... ve ... üçgenlerinin benzerlik oranı ... ise, |FH| uzunluğu ...'ya ve |FB| uzunluğu ...'ye eşit olur.

... ... ... ...

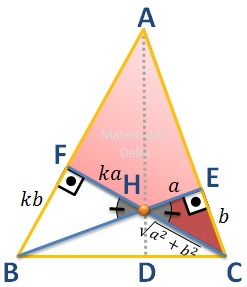
Şimdi de ... ve ... üçgenlerini inceleyelim. ... açısı bu dik üçgenlerde ortaktır. Bu nedenle, ... ve ... açıları eşittir. Tüm açıları eşit olduğu için ... ve ... üçgenleri benzerdir. Benzerlik oranlarını bulabilmek için bu üçgenlerde aynı açının karşısında olan |EC| ve |FC| kenarlarını oranlayabiliriz.

... ... ...

Bu oranı kullanarak |AF| uzunluğunu bulalım.

... ... ...

... ...

|AF| uzunluğunu bulduğumuza göre, ispatın başlarında değindiğimiz ... ve ... üçgenlerinin benzer olup olmadıklarını test edebiliriz.

... ve ... üçgenlerinin ikisi de dik üçgendir. Bu üçgenlerin benzer olabilmeleri için hipotenüs dışındaki kenarların oranlarının eşit olması gerekir.

... ...

Şimdi bu uzunlukları yerlerine koyarak eşitliğin sağlayıp sağlamadığını kontrol edelim. Eşitliğin sol tarafı

... ... ...

oranına eşittir. Sağ taraf ise

... ... ... ...

olur. Eşitlik sağlandığına göre ... ve ... üçgenleri benzerdir ve ... açısı ... açısına eşittir. Bu eşitliği ... üçgeninde kullanırsak, ...'nin 90⁰'ye eşit olduğunu görürüz. Böylece, dar açılı bir üçgende yüksekliklerin aynı noktadan geçtiklerini söyleyebiliriz.

B) Geniş açılı üçgenler

Geniş açılı üçgenlerde yüksekliklerin bir noktada kesiştiğini gösterebilmek için dar açılı üçgenler için elde ettiğimiz sonucu kullanacağız.

Geniş açılı bir üçgende geniş açıyı oluşturan kenarlara ait yükseklikleri ve bu yüksekliklerin uzantılarını çizelim.

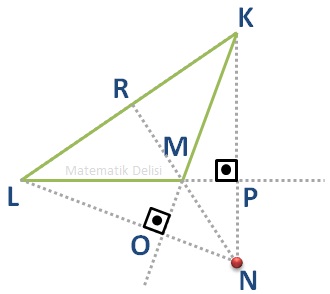
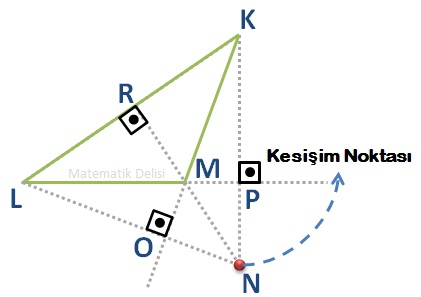
Uzantıların kesiştiği nokta olan N ve geniş açıya sahip olan M köşesinden geçip, karşı kenara kadar ulaşan bir doğru parçası çizelim. Eğer NR doğru parçası KL'ye ait yükseklikse, geniş açılı bir üçgende yüksekliklerin aynı noktada kesiştiğini söyleyebiliriz.

Çizdiğimiz yüksekliklerin uzantılarından oluşan dar açılı ... üçgenini incelediğimizde LP ve KO doğru parçalarının bu üçgenin de yükseklikleri olduğunu görürüz. Önceki kısımdaki çıkarımlarımıza göre KL ve NR arasındaki açının 90 derece olduğunu söyleyebiliriz. Bu açının 90 derece olması, MR'yi ... üçgeninin de yüksekliği haline getirir. Dolayısıyla, geniş açılı bir üçgende yükseklik uzantıları tek bir noktada kesişirler.

C) Dik üçgenler

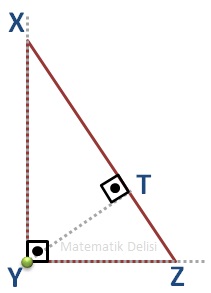
Bu ispattaki en kolay durum üçgenin dik açılı olduğu durumdur.

Dik üçgende hipotenüs dışındaki kenarlar birbirlerine dik oldukları için bu kenarlardan birinin yüksekliği, diğeridir. Bu nedenle yüksekliklerden ikisi dik açının olduğu köşede kesişirler.

Hipotenüsün yüksekliği de dik açılı köşeden geçtiği için bir dik üçgende yüksekliklerin tamamı dik açılı köşeden geçer.