SÜRE
40:002015-2016 TEOG 2. DÖNEM (MAZERET) MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2015-2016 TEOG 2. DÖNEM-MAZERET
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
2–3 + 2–4 işleminin sonucu kaçtır?
2–3 sayısı ...'e ve 2–4 sayısı ...'e eşittir. 23 = 8 ve 24 = 16 olduğu için bulmamız gereken sayı
...
işleminin sonucudur. 5. sınıfta kesirlerin toplamı ile ilgili öğrendiğimiz bilgileri kullanarak, sonucun ...'ya eşit olduğunu görebiliriz.
CEVAP: D
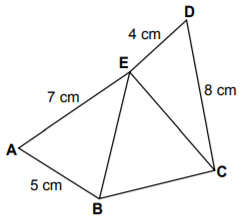
Şekilde verilen ABE ve CDE üçgenlerinde |AB| = 5 cm, |CD| = 8 cm, |DE| = 4 cm, |EA| = 7 cm'dir.
BCE üçgeninin kenar uzunlukları santimetre cinsinden birer tam sayı olduğuna göre bu üçgenin çevresi en az kaç santimetredir?
BCE üçgenindeki kenar uzunluklarının alabileceği en küçük değerleri bulalım.
|BE| :
|BE| uzunluğu, ABE üçgendeki diğer iki kenar uzunluğu arasındaki farktan (7 – 5 = 2 cm'den) büyük olmalıdır. Buna göre |BE|'nin alabileceği en küçük değer 3 cm'dir.
|EC| :
|EC| uzunluğu EDC üçgenindeki diğer iki kenar uzunluğunun farkından (8 – 4 = 4 cm'den) büyük olmalıdır. Dolayısıyla, santimetre cinsinden |EC|'nin alabileceği en küçük tam sayı değeri 5'tir.
|BC| :
|BE| = 3 cm ve |EC| = 5 cm olduğunu varsayarsak, |BC|'nin alabileceği en küçük değer bu iki sayının farkından (5 – 3 = 2 cm'den) büyük olmalıdır. Bu nedenle, seçtiğimiz diğer iki kenar uzunluğunu temel aldığımızda |BC|'nin santimetre cinsinden alabileceği en küçük tam sayı değeri 3 olur.
Çevre Uzunluğu
Yukarıda bulduğumuz değerleri kullanarak çevrenin en az 3 + 5 + 3 = 11 cm olabileceğini görebiliriz.
Not: |BE|'nin uzunluğunu 4 cm olarak seçseydik, |BC| için daha küçük bir değer olan 2 cm'yi kullanabilirdik. Yalnız bu durumda, çevre uzunluğu için yine aynı sonucu elde ederdik.
CEVAP: C
Yukarıdaki işlemlerden hangilerinin sonucu birbirine eşittir?
I) .........
II) ......
III) ......
IV) .........
I ve IV'ün sonuçları aynıdır.
CEVAP: B
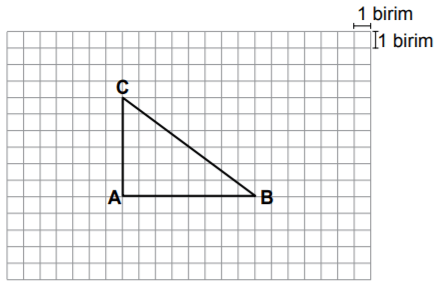
Aşağıdakilerden hangisinde [AT], şekildeki ABC üçgeninin [BC] kenarına ait kenarortayıdır?
ABC dik üçgeninde, [BC] kenarına ait kenarortay, hipotenüsü iki eşit parçaya böler.
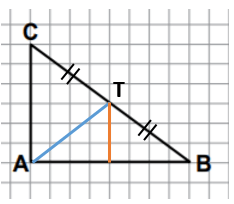
Kenarotayın [CB] kenarıyla kesişim noktasından indirilen dik, ABC üçgenine benzerlik oranı ... olan bir üçgen oluşturur. Buna göre, A ve T noktaları arasındaki yatay uzaklık 8 ÷ 2 = 4 birim ve dikey uzaklık 6 ÷ 2 = 3 birimdir. Bu ölçülere sahip olan doğru parçası A seçeneğinde verilmiştir.
CEVAP: A
Tüm iç açılarının ölçüleri derece cinsinden birer tam sayı olan ABC üçgeninde |AC| < |AB| < |BC| ise ... en fazla kaç derece olabilir?
Bir üçgende büyük açının karşısında uzun kenar ve küçük açının karşısında kısa kenar bulunur.

|AC| < |AB| < |BC| olduğuna göre, açılar arasındaki sıralama ... < ... < ...'dir. Bu üçgendeki en küçük açı ...'dir.
...'nin en büyük değeri için diğer iki açının olası en küçük değerleri alması gerekir. ...'in değerine x dersek, ...'nin değeri en az x + 1 ve ...'nın değeri en az x + 2 olur. Bu üç açının toplamı 3x + 3'tür. Bulduğumuz toplamı 180⁰'ye eşitleyerek ...'nin alabileceği en büyük değeri bulabiliriz.
3x + 3 = 180⁰
⇒ 3x = 177⁰
⇒ x = 59⁰
CEVAP: B

Şekildeki dik koninin taban çapının uzunluğu 24 cm ve |AC| = 18 cm'dir.
Buna göre bu koninin açınımı aşağıdakilerden hangisidir?
Tabanı oluşturan dairenin yarıçapı r = 24 ÷ 2 = 12 cm ve yan yüzü oluşturan daire diliminin yarıçapı l = 18 cm'dir. Daire diliminin açısı ise ... ...'dir.
CEVAP: D
... ve ...olduğuna göre ... ifadesinin değeri kaçtır?
... ... özdeşliğini kullanarakönce ...'nin değerini bulup, daha sonra bu değerin karesini alabiliriz.
... ......
... ...
...
Bulduğumuz değerin karesini alarak sonuca ulaşabiliriz.
... ...... ...
CEVAP: B
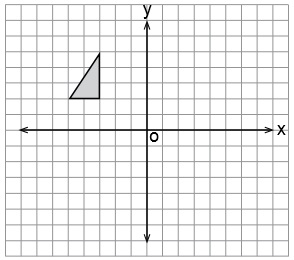
Koordinat düzleminde verilen şeklin orijin etrafında saat yönünde 180° döndürülmesiyle oluşan görüntüsü aşağıdakilerden hangisidir?
Koordinatları (m, n) olan bir nokta orijin etrafında 180° döndürüldüğünde (–m, –n) noktasına gelir. Şekildeki üçgenin tepe noktasının koordinatı (–3, 5)'tir. Üçgen 180° döndürülürse, tepe noktası (3, –5) koordinatına gelir. Sadece C seçeneğindeki şeklin tepe noktası (3, –5)'tir.
CEVAP: C
... ifadesi sadeleştirilebilir bir rasyonel ifade olduğuna göre m'nin alabileceği tam sayı değerlerinin toplamı kaçtır?
Paydanın kökleri x = 3 ve x = –1'dir. Paydaki ifadenin sadeleştirilebilir olabilmesi için bu ifadede x yerine 3 veya –1 yazdığımızda sonucun 0 olması gerekir.
x = 3
32 – m . 3 + 12 = 0
⇒ 9 – 3m + 12 = 0
⇒ 21 – 3m = 0
⇒ 3m = 21
⇒ m = 7
x = –1
(–1)2 – m . (–1) + 12 = 0
⇒ 1 + m + 12 = 0
⇒ m + 13 = 0
⇒ m = –13
Buna göre m'nin alabileceği değerler 7 ve –13'tür. Bu değerlerin toplamı 7 – 13 = –6'dır.
CEVAP: C

Şekildeki ABC ve FDC üçgenlerinde ...'tir.
|AF| = |BC| = 4 cm ve |FC| = 6 cm olduğuna göre |DB| kaç santimetredir?

ABC ve DFC üçgenlerinde, A ve D açıları eşit ve C açısı ortak olduğu için bu üçgenlerdeki tüm iç açılar eşittir. Dolayısıyla, ABC ve DFC üçgenleri benzerdir.
ABC ~ DFC
Benzer üçgenlerde eşit açıların karşılarındaki kenar uzunlukları arasında sabit bir oran vardır. ABC ve DFC üçgenlerinde bu oran
...'tür.
Aynı oran |AC| ve |DC| uzunlukları arasında da bulunmaktadır.
...
⇒ ... cm
|DB| uzunluğu ise, |DC| ile |BC|'nin farkına eşittir.
|DB| = |DC| – |BC| = 15 – 4 = 11 cm
CEVAP: D
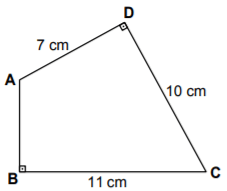
Şekildeki ABCD dikdörtgeninde [AB] ⊥ [BC] ve [AD] ⊥ [DC]'tir.
|AD| = 7 cm, |DC| = 10 cm ve |CB| = 11 cm olduğuna göre |AB| kaç santimetredir?
A ve C noktalarını birleştiren bir doğru parçası çizdiğimizde iki dik üçgen elde ederiz: ADC ve ABC

|AC| uzunluğunu hesaplayabilmek için ADC üçgeninde Pisagor bağıntısını kullanabiliriz.
|AC|2 = |AD|2 + |DC|2=72 + 102 = 49 + 100 = 149 cm2
|AC|2 değerini, ABC üçgeni için kurduğumuz Pisagor bağıntısında yerine yazarak, |AB| uzunluğunu elde edebiliriz.
|AC|2 = |AB|2 + |BC|2
⇒ 149 = |AB|2 + 112
⇒ |AB|2 = 149 – 121
⇒ |AB|2 = 28
⇒ |AB| = ... cm
CEVAP: A
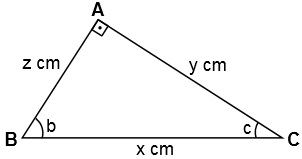
Şekildeki çeşitkenar ABC üçgeninde ... ,... , ... 'dir.
|AB| = ... cm, |BC| = ... cm ve |CA| = ... cm olduğuna göre sin c . cos b aşağıdakilerden hangisine eşittir?
Verilen üçgende hem sin c hem de cos b, ...'e eşittir.Bu ifadelerin çarpımı ...'dir.
CEVAP: C
Bir üçgen dik prizmanın yan yüzlerinin alanları toplamı 108 cm2 dir.
Bu prizmanın yüksekliği 6 cm olduğuna göre tabanlarından biri aşağıdakilerden hangisi olabilir?
Bir üçgen prizmanın yan yüzlerinin alanları toplamı, taban çevresi ile yüksekliğinin çarpımına eşittir. Buna göre, tabandaki üçgenin çevresi 108 ÷ 6 = 18 cm'dir. Çevresi 18 cm olan tek üçgen A seçeneğinde verilmiştir.
CEVAP: A
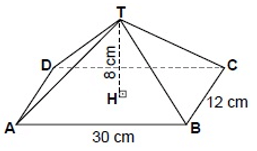
Şekildeki dikdörtgen dik piramidin yüksekliği 8 cm, |AB| = 30 cm ve |BC| = 12 cm'dir.
Buna göre bu piramidin yüzey alanı kaç santimetrekaredir?
Bu piramidin yan yüzleri iki çeşit üçgenden oluşmaktadır. Bu üçgenlerden birinin tabanı 12 cm ve diğerinin tabanı 30 cm'dir. [AB]'nin orta noktasına F ve [BC]'nin orta noktasına E ismini verelim. Üçgenlerin yüksekliklerini bulabilmek için F ve E noktalarını T ve H noktaları ile birleştiren doğru parçaları çizelim.

Ön ve arka yüz
TFH dik üçgeninin hipotenüsü olan [TF] aynı zamanda TAB üçgeninin yüksekliğidir. |TH| = 8 cm ve |HF| = |BC| ÷ 2 = 12 ÷ 2 = 6 cm'dir. Pisagor teoremini kullanarak |TF| uzunluğunun 10 cm'ye eşit olduğu görebiliriz.
|TF|2 = |TH|2 + |HF|2
⇒ |TF|2 = 82 + 62 = 100 cm2
⇒ |TF| = 10 cm
Buna göre ön ve arka yüzlerin her birinin alanı (30 × 10) ÷ 2 = 150 cm2'dir.
Sol ve sağ yüz
Benzer şekilde, TBC üçgeninin yüksekliği olan [TE]'yi bulabilmek için Pisagor teoremini |TH| = 8 cm ve |HE| = 15 cm için kullanabiliriz.
|TE|2 = |TH|2 + |HE|2
⇒ |TE|2 = 82 + 152 = 289 cm2
⇒ |TE| = 17 cm
Buna göre sol ve sağ yüzlerin her birinin alanı (12 × 17) ÷ 2 = 102 cm2'dir.
Taban
Taban alanını 30 × 12 = 360 cm2'dir.
Toplam yüzey alanı
Toplam yüzey alanı
150 + 150 + 102 + 102 + 360 = 864 cm2'dir.
CEVAP: D

Şekilde verilen dokuz noktadan A, B, C, D, E noktaları d doğrusu üzerindedir.
Köşeleri bu dokuz noktadan herhangi üçü olacak biçimde kaç farklı üçgen çizilebilir?
Şekilde verilen 9 noktadan 3 tanesi ... farklı şekilde seçilebilir. Yalnız bu noktaların 3'ü de aynı doğru üzerinde olduğunda üçgen oluşturmayacağı için tüm noktaların d doğrusu üzerinde olduğu durumları çıkarmamız gerekir. d doğrusu üzerindeki 5 noktadan 3'ü ... farklı şekilde seçilebilir. Buna göre, 84 – 10 = 74 üçgen oluşturulabilir.
CEVAP: B

Yukarıdaki şekilde, satranç turnuvasına katılan ve kazanma olasılıkları birbirine eşit olan 8 öğrencinin karşılaşma tablosu verilmiştir.
Yenilenin elendiği turnuvanın finalinde Sevgi ile Barış'ın karşılaşma olasılığı kaçtır?
Sevgi ile Barış'ın finalde karşılaşabilmeleri için her ikisinin de ilk iki karşılaşmasında rakiplerini yenmeleri gerekir. Bu maçların her birinde rakiplerini yenme olasılıkları ... olduğu ve dört maç da birbirinden bağımsız olduğu için istenilen olasılık
... ... ... 'dır.
CEVAP: B
a > 0 ve b < 0 olduğuna göre denklemi ax + by + c=0 olan doğrunun grafiği aşağıdakilerden hangisi olabilir?
Denklemi ax + by + c = 0 olan doğrunun eğimi ...'dir. a pozitif ve b negatifse, eğim pozitif çıkar. Pozitif eğime sahip olan tek doğru A seçeneğinde verilmiştir.
B seçeneğindeki doğrunun eğimi negatif; C seçeneğindeki doğrunun eğimi 0; ve D seçeneğindeki doğrunun eğimi tanımsızdır.
CEVAP: A
Altuğ parasının ...'i ile bir kalem,...'si ile bir defter satın alıyor.
Geriye 4 lirası kaldığına göre defterin fiyatı kaç liradır?
Altuğ'un başlangıçtaki parasına x dersek,
Harcadığı toplam para
.........'tir.
Başlangıçtaki parası x olduğu için harcamaları yaptıktan sonra kalan parası
... olur.
x cinsinden bulduğumuz bu değer, 4'e eşittir.
... lira
Bu denklemin iki tarafını da 4'e böler, 15'le çarparsak, x = 15 lira sonucuna ulaşırız.
Altuğ'un parası 15 lira olduğuna göre, defterin fiyatını bulabilmek için 15'in ...'ini hesaplarız.
... lira
CEVAP: D
ax + by = 9
ax – by = 3
denklem sistemini sağlayan (x, y) sıralı ikilisi (3, 1) olduğuna göre a + b kaçtır?
Denklem sistemini (3, 1) ikilisi sağladığına göre, x yerine 3 ve y yerine 1 yazdığımızda, sistemdeki eşitliklerin sağlamaya devam etmesi gerekir. Bu işlemi yaptığımızda karşımıza yeni bir denklem sistemi çıkar.
3a + b = 9
3a – b = 3
Bu denklem sistemini çözebilmek için iki denklemi de taraf tarafa toplayabiliriz.
3a + b + 3a – b = 9 + 3
⇒ 6a = 12
⇒ a = 2
a = 2 sonucunu ilk denklemde yerine yazarak b'nin değerini de bulabiliriz.
3 . 2 + b = 9
⇒ b = 3
Buna göre a + b = 2 + 3 = 5'tir.
CEVAP: C
x tam sayısı, y tam sayısının 2 katının 10 eksiğine eşittir. 8-A sınıfının mevcudu ... ve 8-B sınıfının mevcudu y'dir.
8-A sınıfının mevcudu 8-B sınıfının mevcudundan fazla olduğuna göre 8-B sınıfının mevcudu en az kaçtır?
Sorudaki eşitsizlik, ... > ...'dir.
x sayısı y'nin 2 katının 10 eksiğine eşit olduğuna göre yukarıdaki eşitsizlikte x yerine 2y – 10 yazabiliriz.
... > ...
Bu eşitsizliği çözebilmek için önce soldaki 9'u sağ tarafa atarız.
... > ...
Sol taraftaki kesrin paydasından kurtulabilmek için 2'yi karşı tarafa atarız.
... > ...
Parantezleri açtığımızda aşağıdaki eşitsizliği elde ederiz.
... > ...
Bir tarafta değişkenleri ve diğer tarafta sabit sayıları toplarız.
... > ...
Sağ ve sol taraftaki işlemleri yaparız.
... > ...
Soldaki y'yi yalnız bırakabilmek için katsayısını sağa atarız.
... > ...
y değişkeni 12'den büyük bir tam sayı olduğuna göre, bu değişkenin alabileceği en küçük değer 13'tür.
CEVAP: B