BÖLÜM 2: ÜÇ ÖNEMLİ ÖZDEŞLİK
Aşağıdaki 3 özdeşliği bilmemiz bazı problemlerin çözümünde oldukça faydalı olacaktır.
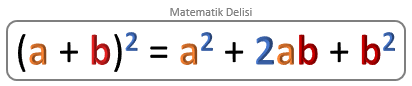
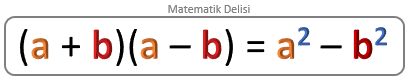
ÖZDEŞLİK 1
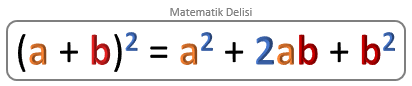
Eşitliğin sol tarafındaki kareyi daha açık bir şekilde yazalım.
(
Çarpmanın dağılma özelliğini kullanarak parantezlerden kurtulalım.
(
=
=
Böylece eşitliğin sağ tarafındaki ifadeyi elde ediyoruz.
ÖZDEŞLİK 2
Sol taraftaki kareyi açık haliyle yazalım.
(
Parantezleri açalım.
(
=
=
Eşitliğin sol tarafını daha açık şekilde yazdığımızda sağ tarafındaki ifadeyi elde ettiğimiz için bu bir özdeşliktir.
ÖZDEŞLİK 3
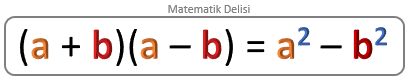
Eşitliğin solundaki parantezi açalım.
(
=
=
ÖZDEŞLİKLERİN FARKLI BİÇİMLERİ
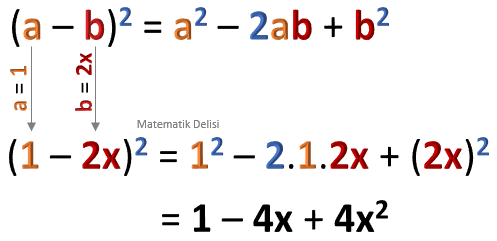
Yukarıda özdeşliklerde,
Ayrıca bir özdeşlikte
- sağ ve sol tarafları yer değiştirmemiz veya
- bir taraftaki terimleri kendi aralarında yer değiştirmemiz
bu eşitliğin özdeşlik olduğu gerçeğini değiştirmez.
Aşağıdaki eşitlikler yukarıda öğrendiğimiz özdeşliklerin farklı biçimleridir.
- (x – y)2 = x2 – 2xy + y2
- (1 + x)2 = 1 + 2x + x2
- (x + 1)2 = 1 + x2 + 2x
- (5 + a)(a – 5) = a2 – 25
- 36 – x2 = (6 + x)(6 – x)
- (10 – x)2 = 100 + x2 – 20x
- 4 + 4y + y2 = (y + 2)2
Aşağıdaki eşitliklerden hangileri özdeşliktir?
a) (1 – x)(x + 1) = x2 – 1
b) 4 – 4x – x2 = (x – 2)2
c) (x + 3)2 – x2 = 6x + 9
d) (a – x)2 = –2ax + x2 + a2
e) (4 + z)2 = z2 + 16 + 8z
f) (a – 1)2 = b2 – 2b + 1
g) (1 + x)(x + 1) = 2x + 1 + x2
