BÖLÜM 3: ÖZDEŞLİKLER NASIL KULLANILIR?
Önceki bölümde öğrendiğimiz 3 önemli özdeşliği nasıl kullanabileceğimize dair örnekleri aşağıda bulabilirsiniz.
ÖZDEŞLİK 1
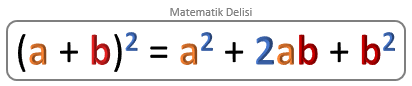
İlk özdeşlik, 2 sayının toplamı, çarpımı ve karelerinin toplamı arasında bir ilişki kurmaktadır.
Bu değerlerden ikisi verilip, üçüncüsü istendiğinde yukarıdaki özdeşliği kullanabiliriz.
Kareleri toplamı 85 olan iki sayının toplamı 11 ise bu sayıların çarpımı kaçtır?
Bu sayılara
Verilen değerleri
(
özdeşliğinde yerlerine yazdığımızda
11
eşitliğini elde ederiz. Bu eşitliğin sağlanabilmesi için
Aşağıdaki boşluklara uygun sayıları yazalım.
... ... |
||
|---|---|---|
| Toplam | Çarpım | Kareleri Toplamı |
| 4 | 3 | ... |
| 4 | ... | 8 |
| ... | 33 | 130 |
| 16 | ... | 130 |
| 16 | 15 | ... |
ÖZDEŞLİK 2
Bu özdeşlik, iki sayının farkı, çarpımı ve karelerinin toplamı arasında bir ilişki kurmaktadır.
Bir soruda yukarıdakilerden ikisi verilip üçüncüsü istenebilir.
Kareleri toplamı 52 olan iki sayının çarpımı 24'e eşitse bu sayıların farkı kaçtır?
Bu sayılara
Bu değerleri
(
özdeşliğinde yerlerine koyarsak
(
sonucunu elde ederiz. Her iki tarafın da karekökünü alarak bu sayıların farkının
Aşağıdaki boşluklara uygun sayıları yazalım.
... ... |
||
|---|---|---|
| Fark | Çarpım | Kareleri Toplamı |
| 1 | ... | 25 |
| 1 | 90 | ... |
| ... | 36 | 153 |
| 2 | ... | 74 |
| ... | 64 | 128 |
ÖZDEŞLİK 3
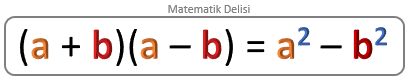
Bu özdeşliği pay ve paydada verilen ifadeleri sadeleştirmek için kullanabiliriz.
... ... ...
Aynı özdeşliği, büyük sayıların kareleri arasındaki farkı kolay hesaplayabilmek için de kullanabiliriz.
- 18122 – 18022 = (1812 – 1802)(1812 + 1802) = 10 . 3614 = 36 140
- 100 0012 – 99 9992 = (100 001 – 99 999)(100 001 + 99 999) = 2 . 200 000 = 400 000
- 362 – 322 = (36 – 32)(36 + 32) = 4 . 68 = 272
ALIŞTIRMALARIN CEVAPLARI
| Toplam | Çarpım | Kareleri Toplamı |
| 4 | 3 | |
| 4 | 8 | |
| 33 | 130 | |
| 16 | 130 | |
| 16 | 15 |
| Fark | Çarpım | Kareleri Toplamı |
| 1 | 25 | |
| 1 | 90 | |
| 36 | 153 | |
| 2 | 74 | |
| 64 | 128 |
