BÖLÜM 1: ÖZDEŞLİK NEDİR? BİR EŞİTLİĞİN ÖZDEŞLİK OLUP OLMADIĞINI NASIL ANLARIZ?

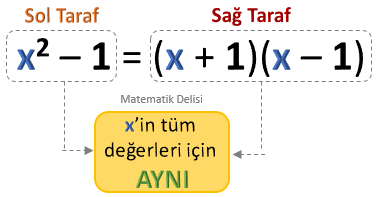
ÖZDEŞLİK: Bir eşitliğin sağ ve sol tarafları, değişkenlerin alabileceği tüm değerler için aynıysa, bu eşitlik bir özdeşliktir.

ÖRNEK:

x(x + 1) = x² + x eşitliği bir özdeşliktir.

Bu bir özdeşlikse, x'in tüm değerleri için eşitliğin sağ ve sol taraflar aynı olmalıdır. Birkaç farklı değer için bunu test edelim.

(x = 0)

x yerine 0 yazdığımızda

Eşitliğin sol tarafı 0(0 + 1) = 0 ve
Eşitliğin sağ tarafı 0² + 0 = 0 olur.

(x = 1)

x yerine 1 yazdığımızda

Eşitliğin sol tarafı 1(1 + 1) = 2 ve
Eşitliğin sağ tarafı 1² + 1 = 2 olur.

Yukarıdakilere benzer şekilde x yerine yazdığımız tüm değerler için eşitliğin sağ ve sol taraflarının aynı çıktığını görebiliriz. Bu denklem bir özdeşliktir.

ÖRNEK:

Aşağıdaki eşitlikler, özdeşliktir.

x = x
2x – 6 = 2(x – 3)
(x + 1)(x + 2) = x² + 3x + 2

BİR EŞİTLİĞİN ÖZDEŞLİK OLUP OLMADIĞINI NASIL ANLARIZ?

Bir eşitliğin özdeşlik olup olmadığını anlayabilmek için aşağıdaki adımları izleyebiliriz.

Parantezli ifadeleri açar, çarpma işlemlerini yaparız. Benzer terimler arasında toplama ve çıkarma işlemleri yaparak eşitliğin sağ ve sol tarafındaki ifadelerin en sade hallerini buluruz.
Bu işlemler sonucunda elde ettiğimiz eşitlikte
- Sağ ve sol taraftaki terimlerin tümü aynıysa, bu eşitlik bir özdeşliktir.
- Sağ ve sol taraftaki terimlerin katsayıları farklıysa veya bir taraftaki bir terim diğer tarafta yoksa, bu eşitlik bir özdeşlik değildir.

ÖRNEK:

2x – 6 = 2(x – 3) eşitliğinin özdeşlik olup olmadığını test edelim.

Eşitliğin sağındaki parantezi açalım.

2(x – 3) = 2x – 6

Bulduğumuz ifade, denklemin sol tarafı ile aynıdır.

2x – 6 = 2x – 6

İki tarafta da aynı terimler olduğu için bu eşitlik bir özdeşliktir.

Özdeşlik örnekleri için tıklayın.

ÖRNEK:

3(x – 1) = 2(x – 2) eşitliğinin özdeşlik olup olmadığı bulalım.

Eşitliğin sağındaki ve solundaki parantezleri açalım.

Eşitliğin solu: 3(x – 1) = 3x – 3
Eşitliğin sağı: 2(x – 2) = 2x – 4

Buna göre

3x – 3 = 2x – 4

olmalıdır. Yalnız bu eşitlikte sol ve sağ taraftaki terimlerin katsayıları aynı değildir. Örneğin, solda 3x olduğu halde sağda 2x bulunmaktadır. İki tarafta farklı terimlerle karşılaştığımız için bu eşitlik bir özdeşlik değildir.

Özdeşlik örnekleri için tıklayın.

Alıştırmalar-1

Aşağıdaki eşitliklerden hangileri özdeşliktir?

a) a(a – b) = a² – b²

b) (x – 1)(x + 1) = x² – 1

c) 3(a² + a) = a(3a + 3)

d) y² – 1 = (1 – y)(y – 1)

e) x = y

f) (x – 1)(x + 2) = x² + x – 2

CEVAPLAR

ALIŞTIRMALARIN CEVAPLARI

Alıştırmalar-1