BÖLÜM 1: CEBİRSEL İFADELERDE PARANTEZE ALMA
ORTAK PARANTEZE ALMA
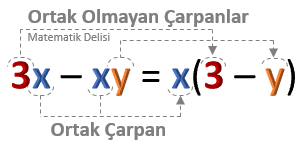
Cebirsel ifadelerde, terimleri ortak çarpan parantezine alabilmek için önce hangi çarpanların
tüm terimlerde ortak olduğunu saptarız. Daha sonra
- Parantez dışına, bulduğumuz ortak çarpanları yazarız.
- Parantez içine, ifadeyi ortak çarpanlara böldüğümüzde ortaya çıkan sonucu yazarız.
Bir cebirsel ifadeyi ortak çarpan parantezine aldığımızda, çarpanlarına ayırmış oluruz. Sonraki konuda, cebirsel ifadeleri çarpanlara ayırmak için kullandığımız farklı yöntemleri öğreniyoruz.
Yukarıdaki cebirsel ifadede iki terim var:
x 2 terimi iki tanex 'in çarpımına eşittir:x 2 =x .x x y terimi isex iley 'nin çarpımına eşittir:x y =x .y
Bu terimlerin ortak çarpanı
- parantez dışına,
x değişkenini ve - parantez içerisine,
x çarpanı atıldığında terimlerden geriye kalan ifadeyi yazarız.
Parantez içerisine yazacağımız ifadeyi bulabilmek için terimleri tek tek ortak çarpana böleriz.
x 2'den bir tanex çarpanını atarsak, geriyex kalır.x y 'denx çarpanını atarsak, geriyey kalır.
Terimlerden geriye kalan ifadeleri birleştirdiğimizde karşımıza
Özetle,
- Parantezin dışında,
x ve - Parantez içinde,
x +y yazarız.
Matematiksel olarak, paranteze alma işlemini aşağıdaki gibi gösteririz.
Yukarıdaki örnekte gördüğümüz paranteze alma işlemini geometrik olarak da yorumlayabiliriz.
- Kenar uzunluğu
x olan bir karenin alanıx 2'dir. - Kenar uzunlukları
x vey olan bir dikdörtgenin alanı isex y 'dir.
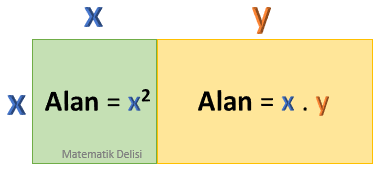
Bu iki şeklin alanları toplamı
a 2b terimi, 2 tanea ve 1 taneb 'nin çarpımına eşittir:a 2b =a .a .b b 2a terimi, 2 taneb ve 1 tanea 'nın çarpımına eşittir:b 2a =b .b .a
İki terimde de bir
- Ortak
a b parantezine alınmış ifadede, parantez dışındaa b bulunmalıdır. - Parantez içerisine ise, terimleri tek tek
a b 'ye bölündüğümüzde bulduğumuz ifadeyi yazmamız gerekir.
İlk Terim: İlk terimde iki
a ve birb çarpanı bulunuyor. Eğer bu çarpanlardan bira ve birb 'yi çıkarırsak, geriye sadece bir tanea kalır. Başka bir deyişle,a 2b teriminia b 'ye böldüğümüzdea sonucunu buluruz. Bu nedenle parantez içerisindeki ilk terimin yerinea yazmamız gerekir....
İkinci Terim: Bir
a ve ikib çarpanı olan ikinci terime de aynı bölme işlemini uyguladığımızda,b sonucunu elde ederiz....
Kısacası, parantez dışında
NOT: Aynı ifadeyi yalnız
Aşağıdaki cebirsel ifadelerdeki ortak çarpanları bulup, bu ifadeleri ortak çarpan parantezine alın.
a) –x2y + xy = ...
b) x3 + x2y = ...
c) –a3b2 – a2b = ...
d) m3 + m2 = ...
e) x – x18 = ...
Şu ana kadar sadece 2 terim içeren ifadeleri ortak çarpan parantezine aldık. Aynı işlemleri 3 veya daha fazla terim
içeren cebirsel ifadeler için de yapabiliriz.
Yukarıdaki terimlerin tümünün ortak çarpanı
- İlk terimin
m n 'ye bölümüm 'dir. - İkinci terimin
m n 'ye bölümü –n 2'dir. - Üçüncü terimin
m n 'ye bölümü 1'dir.
Bu nedenle parantez içerisindeki ifade
Aşağıdaki cebirsel ifadelerdeki ortak çarpanları bulup, bu ifadeleri ortak çarpan parantezine alın.
a) x3 – x2 + x = ...
b) x2y + xy2 + x = ...
c) –x3y2 + x4 – x2y2 = ...
d) a2b2 + ab2 + b2 = ...
e) a3 – a2b – ab2 – a4b3 = ...
Sadece değişken kısımlardaki değil, aynı zamanda katsayılardaki ortak çarpanları da parantez dışına
yazabiliriz.
Yukarıdaki ifadenin terimlerine baktığımızda, değişken kısımların ortak çarpanının
Aşağıdaki cebirsel ifadelerdeki ortak çarpanları bulup, bu ifadeleri ortak çarpan parantezine alın.
a) 15x2 – 5x = ...
b) 12xy + 6x2 – 9xy2 = ...
c) 3a2 – 9a + 27a3 = ...
d) –10xy2 + 25x2y = ...
e) 12a3 + 6a2 – 3a5 = ...
Yukarıdaki örneklerin tümünde, ortak çarpanın işaretinin "
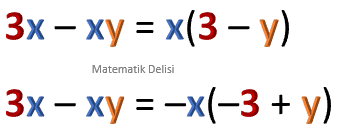
Ortak çarpanın işaretini "
–
Yukarıdaki ifadeyi ortak
–
Aynı ifadeyi –
–
Aşağıdaki boşlukları uygun ifadelerle doldurun.
a) x2 – 2x3 + x = –x(.......)
b) –x2y + xy – xy2 = –xy(.......)
c) a3b3 – a2b2 = –a2b2(.......)
d) a3b3 – a2b2 = a2b2(.......)
e) a2 – ab + a2b2 = –a(.......)
ALIŞTIRMALARIN CEVAPLARI
a) xy(–x + 1), b) x2(x + y), c) a2b(–ab – 1), d) m2(m + 1), e) x(1 – x17)
a) x(x2 – x + 1), b) x(xy + y2 + 1), c) x2(–xy2 + x2 – y2), d) b2(a2 + a + 1), e) a(a2 – ab – b2 – a3b3)
a) 5x(3x – 1), b) 3x(4y + 2x – 3y2), c) 3a(a – 3 + 9a2), d) 5xy(–2y + 5x), e) 3a2(4a + 2 – a3)
a) –x + 2x2 – 1, b) x – 1 + y, c) –ab + 1, d) ab – 1, e) –a + b – ab2
