BÖLÜM 2: TERİMLERİN ÇARPIMI
Üslü sayılarla işlemler konusundan hatırlayacağınız gibi, tabanı eşit olan üslü ifadeleri
çarptığımızda, kuvvetleri topluyorduk. Bu kural, tabanı değişken olan üslü ifadeler için de geçerlidir.
Aşağıdaki çarpma işlemlerinde tabanlar aynı olduğu için üsler toplanmıştır.
x 2 .x 3 =x 2 +3 =x 5a 3 .a =a 3 + 1 =a 4y .y =y 1 + 1 =y 2
Yukarıdaki kurala ek olarak, çarpmanın değişme özelliğini de (
4x2 ile 6x3 terimlerini çarpalım.
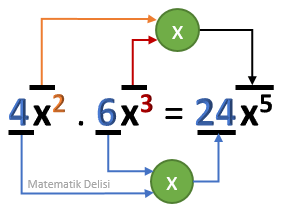
- Katsayıların kendi aralarında çarpımı
4 .6 =24 'e ve - Üslü ifadelerin kendi aralarında çarpımı ise x
2 . x3 = x5'e eşittir.
Sonuç olarak, verilen terimlerin çarpımı
3x2y ile 2xy2 terimlerini çarpalım.
3
- iki katsayı: 3 ve 2
- tabanı
x olan iki üslü ifade:x 2 vex - tabanı
y olan iki üslü ifade:y vey 2
görüyoruz. Bu çarpanları kendi aralarında çarpıp, sonucu tek bir terim halinde yazabiliriz.
- Katsayıların çarpımı 3 . 2 = 6 yapar.
- Tabanı
x olan üslü ifadelerin çarpımıx 2 .x =x 3'e eşittir. - Tabanı
y olan üslü ifadelerin çarpımıy .y 2 =y 3'e eşittir.
Sonuç olarak, verilen terimlerin çarpımı 6
3
- x . 6y3 = 6xy3
- a2 . a3 = a5
- a . 2a2b = 2a3b
- a2b . ba4 = a6b2
- x2yz . xy2z = x3y3z2
Aşağıdaki çarpma işlemlerinin sonuçlarını bulun.
a) 5x . 15x6 = ... b) 4x2y2 . 2xy2 = ... c) a3 . 3a = ... d) a2b5 . 8ab = ... e) xy2z3 . 4x2yz5 = ...
