BÖLÜM 3: CEBİRSEL İFADELERİN ÇARPIMI

![]() İki cebirsel ifadeyi birbiriyle çarparken
İki cebirsel ifadeyi birbiriyle çarparken
- Bu ifadeleri parantez içerisine alıp, çarpım halinde yazarız.
- Çarpmanın dağılma özelliğini kullanarak, parantezleri açarız.
- Benzer terimler arasında toplama ve çıkarma işlemlerini yaparız.
x ile x2 + 3x ifadelerini çarpalım.
Bu iki ifadenin çarpımını aşağıdaki gibi gösterebiliriz.
(
Yalnız, ilk ifade tek terimden oluştuğu ve başında "–" işareti olmadığı için bu ifadeyi parantez içerisine almadan da yazabiliriz.

Parantezi açmak için parantez dışındaki
x2y + y ile xy ifadelerini çarpalım.
Bu ifadelerin çarpımını aşağıdaki gibi yazabiliriz.
(
Ayrıca, ikinci ifade pozitif ve tek terimli olduğu için parantez içerisine yazılıp yazılmaması işlem sonucunu değiştirmez.
(
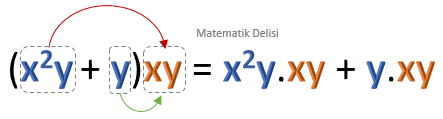
Parantez içerisindeki terimleri tek tek ikinci ifade ile çarparak, parantezden kurtulabiliriz.
(
x + 1 ve x + 2 ifadelerini çarpalım.
Çarpacağımız ifadelerin her birinde iki terim bulunuyor. İki ifadeyi de parantez içerisine alalım.
(
Çarpma işlemindeki parantezlerden kurtulabilmek için sırasıyla aşağıdaki adımları izleyebiliriz.
- İlk parantezin ilk terimini, ikinci parantezdeki terimlerle tek tek çarparız.
- İlk parantezin ikinci terimini, ikinci parantezdeki terimlerle tek tek çarparız.
- Bulduğumuz çarpım sonuçlarını toplarız.

(
=
= x2 + 2x + x + 2
= x2 + 3x + 2
Yukarıdakine benzer çarpma işlemlerinde ilk iki adımı birleştirebiliriz. Sonucu bulabilmek için ilk parantezdeki her terimi, ikinci parantezdeki her bir terimle tek tek çarparak, toplamamız yeterli olacaktır.
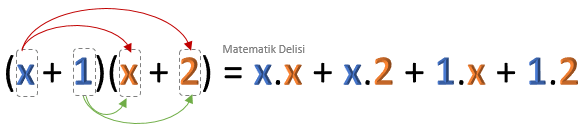
![]() Parantezi açarken terimleri işaretleriyle beraber çarptığımıza dikkat etmemiz gerekir.
Parantezi açarken terimleri işaretleriyle beraber çarptığımıza dikkat etmemiz gerekir.
–x + 1 ve x – 2 ifadelerini çarpalım.
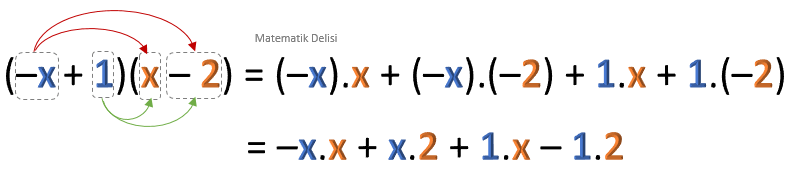
(
= (–
= –x2 + 2x + x – 2
= –x2 + 3x – 2
- –4a(a – 2a2) = –4a2 + 8a3
- (b – 4)b2 = b3 – 4b2
- (2x + 1)(2x – 2) = 4x2 – 2x – 2
- (x – 3)(2x – 2) = 2x2 – 8x + 6
- (xy2 – 1)(x2y + 1) = x3y3 + xy2 – x2y – 1
Aşağıdaki çarpma işlemlerinin sonuçlarını bulun.
a) 3x2y(x + y) = ...
b) (x2 + 1)x = ...
c) (x + 1)(x + 1) = ...
d) (x – y)(x + y) = ...
e) (a2 – b)(b2 – a) = ...
ALIŞTIRMALARIN CEVAPLARI
a) 3x3y + 3x2y2, b) x3 + x, c) x2 + 2x + 1, d) x2 – y2, e) a2b2 – a3 – b3 + ab
