ÇIKMIŞ SORULAR: ARALARINDA ASAL SAYILARLA İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ
Aralarında asal sayılar ile ilgili LGS'de (Liselere Giriş Sınavında) çıkan soruları ve bu soruların çözümlerini aşağıda bulabilirsiniz.
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 0 |
| 2018-2019 | 0 |
| 2019-2020 | 0 |
| 2020-2021 | 1 |
| 2021-2022 | 0 |
| 2022-2023 | 1 |
| 2023-2024 | 0 |
(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)
2020-2021 LGS
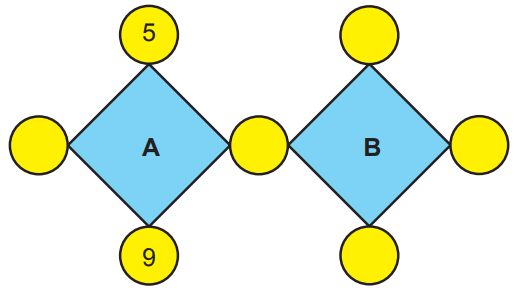
Yukarıdaki şekilde verilen her bir dairenin içine birbirinden farklı birer doğal sayı yazılacaktır. Bu sayılardan ikisi şekilde verilmiştir. Bulundukları dörtgenin köşelerindeki dairelerde yazan dört sayının çarpımına eşit olan A ve B sayıları aralarında asaldır.
Buna göre A + B en az kaçtır?
Çözüm:
Çözümü daha iyi takip edebilmek için verilen boşlukları isimlendirelim.
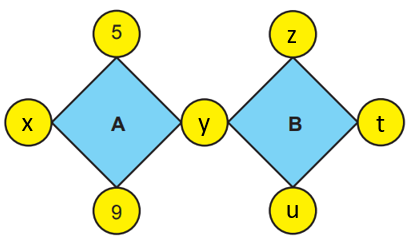
y sayısı hem A hem de B'nin köşesinde olduğundan iki sayının da çarpanıdır. Yalnız, aralarında asal olan A ve B sayılarının tek ortak çarpanı 1'dir. Bu nedenle y = 1 olmalıdır.
A + B'nin en düşük değerini aradığımız için diğer boşluklara da mümkün olduğunca küçük sayılar yazmamız gerekir. 2, 3 ve 4 sayılarını bu boşluklara yerleştirmeye çalışalım.
A'nın alt köşesinde 9 olduğu için bu sayı 9'a ve dolayısıyla 3'e kalansız bölünür. z, t veya u yerine 3 yazmamız, B'yi de 3'e bölünebilir yapar. Bu durumda A ve B aralarında asal olmaz. Dolayısıyla 3'ü yalnızca x yerine yazabiliriz. z ve t'nin bulunduğu dairelere de 2 ve 4 sayılarını yerleştirebiliriz.
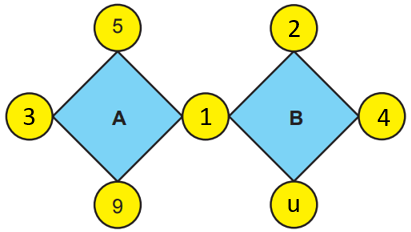
Şimdi de geriye kalan son boşluğa yazabileceğimiz en küçük sayıyı bulalım. Halihazırda A'nın çarpanlarından biri 5 olduğu için bu sayıyı u yerine yazamayız. 6 sayısı ise 3'e kalansız bölünür. Bu nedenle, u yerine 6 yazmamız A ile B'nin aralarında asal olmasını engeller. Yalnız, şekildeki herhangi bir sayı 7'nin tam katı olmadığı için u yerine 7 yazabiliriz.
Yukarıda bulduğumuz sayıları kullandığımızda A'nın 135'e ve B'nin 56'ya eşit olduğunu görebiliriz.
A = 3 . 5 . 1 . 9 = 135
B = 1 . 4 . 7 . 2 = 56
Buna göre A + B toplamı en az 191'dir.
135 + 56 = 191
CEVAP: B
2022-2023 LGS
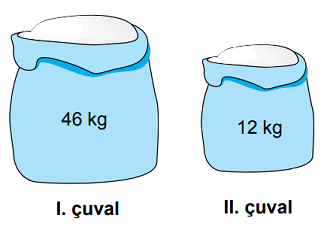
Yukarıda iki adet un çuvalı ve bu çuvallarda bulunan un miktarları verilmiştir. Bu çuvallara belli miktarlarda un eklendiğinde çuvallardaki un miktarlarının kilogram cinsinden değerleri, aralarında asal olmaktadır.
Buna göre, çuvallara eklenen un miktarlarının kilogram cinsinden değerleri aşağıdakilerden hangisi olabilir?
| I. çuval | II. çuval | |
|---|---|---|
| 5 | 4 | |
| 8 | 6 | |
| 3 | 2 | |
| 9 | 3 |
Çözüm:
Seçeneklerde verilen miktarları çuvallara eklediğimizde, kilogram cinsinden yeni miktarlar aşağıdaki gibi olur.
| I. çuval | II. çuval | |
|---|---|---|
| 46 + 5 = 51 | 12 + 4 = 16 | |
| 46 + 8 = 54 | 12 + 6 = 18 | |
| 46 + 3 = 49 | 12 + 2 = 14 | |
| 46 + 9 = 55 | 12 + 3 = 15 |
- B seçeneğinde elde ettiğimiz sayılar 6'ya,
- C seçeneğinde elde ettiğimiz sayılar 7'ye ve
- D seçeneğinde elde ettiğimiz sayılar 5'e
kalansız bölünür.
A seçeneğindeki sayıların ortak çarpanı yoktur. 51 ile 16 sayıları aralarında asaldır.
CEVAP: A
