BÖLÜM 2: ÜÇGENLERİN BENZER OLUP OLMADIKLARI NASIL ANLAŞILIR?
Aşağıdaki 3 şarttan herhangi birine uyan üçgenler benzerdir.
Önceki bölümde yaptığımız benzer üçgen tanımı aşağıdaki
şartlardan ilkinde verilmiştir.
Diğer iki şart da benzerliği tanımlamak için kullanılabilir.
1) İÇ AÇILAR
İç açıları eşit olan üçgenler benzerdir.
İç açıları eşit olan üçgenler arasındaki benzerlik, Açı-Açı-Açı benzerliği (AAA) olarak adlandırılabilir.
İç açılarından ikisi eşit olan üçgenlerin üçüncü iç açıları da eşit olacağından,
iki iç açının eşit olması da benzerlik şartı olarak kabul edilebilir. Bu nedenle
aynı benzerlik bazen Açı-Açı benzerliği (AA) olarak da adlandırılır.
...
...
...
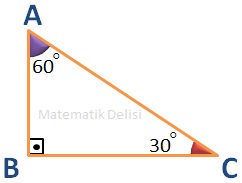
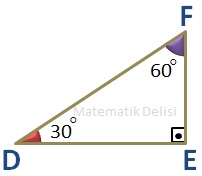
Yukarıdaki ... ve ... üçgenlerinin iç açıları eşit olduğu için, bu üçgenler benzerdir.
...
2) KENAR UZUNLUKLARI
Kenar uzunlukları arasında sabit bir oran bulunan üçgenler benzerdir.
Üçgenlerin kenar uzunlukları arasındaki sabit orandan dolayı benzer olması durumuna Kenar-Kenar-Kenar benzerliği (KKK) ismi verilir.
Benzer üçgenlerin kenar uzunlukları arasındaki orana benzerlik oranı ismi verilir.
......
......
......
... üçgeninin kenar uzunlukları, ... üçgeninin kenar uzunluklarının 2 katıdır. Bu nedenle, ...'dir.
Aşağıda 8 farklı üçgenin kenar uzunlukları verilmiştir. Bu üçgenlerden hangileri benzerdir?
a) |AB| = 5, |BC| = 6, |CA| = 7
b) |DE| = 2, |EF| = 2, |FD| = 3
c) |GH| = 2, |HI| = 4, |IG| = 4
d) |JK| = 12, |KL| = 14, |LJ| = 10
e) |MN| = 3, |NO| = 5, |OM| = 5
f) |PR| = 6, |RS| = 6, |PS| = 3
g) |TU| = 6, |UV| = 8, |VT| = 9
h) |XY| = 12, |YZ| = 9, |XZ| = 15
3) BİR İÇ AÇI VE BU AÇIYI OLUŞTURAN İKİ KENAR UZUNLUĞU
İç açılarından biri eşit olan ve bu açıyı oluşturan iki kenar uzunluğu arasında sabit bir oran bulunan üçgenler benzerdir.
Bu benzerlik türü, Kenar-Açı-Kenar benzerliği (KAK) olarak adlandırılır.
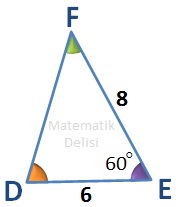
Yukarıdaki üçgenlerde değeri gösterilen açıların eşit olduklarını görüyoruz.
...
Bu üçgenlerin benzer olup olmadıklarını anlamak için ... ve ... açılarını oluşturan kenarların uzunlukları arasındaki oranlara bakmamız gerekiyor.
......
......
Kenar uzunlukları arasında sabit bir oran olduğu için ... ve ... üçgenleri benzerdir.
...
Aşağıda 7 üçgenin birer açısı ve bu açıyı oluşturan kenarların uzunlukları verilmiştir. Bu üçgenlerden hangileri benzerdir?
a) ..., |AB| = 4, |AC| = 8
b) ..., |ED| = 6, |EF| = 12
c) ..., |GH| = 8, |HI| = 16
d) ..., |JK| = 9, |KL| = 15
e) ..., |NO| = 6, |MN| = 6
f) ..., |PR| = 8, |RS| = 8
g) ..., |UV| = 4, |UT| = 8
İki açı ve bir kenar uzunluğunun aynı olması üçgenlerin benzerliğini gösterir mi? Açı-Kenar-Açı benzerliği var mı?
Açılardan ikisinin aynı olması üçüncü açıların da aynı olacağı anlamına gelir. Bu nedenle iki açısı aynı olan üçgenler, kenar uzunluklarından biri aynı olmasa dâhi benzerdir. Bu duruma Açı-Açı benzerliği diyoruz. Ayrıca bir Açı-Kenar-Açı benzerliği tanımlamamıza bizce gerek yoktur.
Yukarıda anlatılan benzer olma koşullarından birinin doğru olması, diğer şartların da
doğru olduğu anlamına gelir.
İki üçgenin iç açıları aynı ise, aynı açının karşısındaki kenar uzunluklarının oranı sabittir;
kenar uzunlukları arasında sabit bir oran bulunan üçgenlerin iç açıları aynıdır.
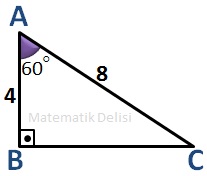
... üçgenindeki |DF| uzunluğunu bulalım.
Önce ... ve ... üçgenlerinde verilmeyen açıları bulalım.
... üçgenindeki ... açısı 30⁰'dir.
... ...
... üçgenindeki ... açısı ise 60⁰'dir.
... ...
Böylece tüm iç açıların aynı olduğunu görüyoruz. İç açıları aynı olan üçgenler benzerdir. Aynı açıya sahip köşeleri aynı sırayla yazarak, bu benzerliği
...
ile gösterebiliriz.
Bu üçgenler benzer olduğu için aynı açının karşısındaki kenarların oranı da sabit olmalıdır. ... üçgeninde 90⁰'lik açının karşısındaki kenar 8 ve ... üçgeninde aynı açının karşısındaki kenar 6 birimdir. Bu nedenle benzerlik oranı ...'tür. Bu oran 30⁰'lik açının karşısındaki kenarlar için de geçerlidir. |AB| ile |DF|'yi oranlayıp ...'e eşitleyerek |DF| uzunluğunu bulabiliriz.
... ...
Bulduğumuz eşitlik |DF|'nin 3'e eşit olduğunu gösterir.
ALIŞTIRMALARIN CEVAPLARI
a ile d seçeneklerinde verilen üçgenler benzerdir.
...
c ile f seçeneklerinde verilen üçgenler benzerdir.
...
a ile c seçeneklerinde verilen üçgenler benzerdir.
...
e ile f seçeneklerinde verilen üçgenler benzerdir.
...
