ÇIKMIŞ SORULAR: ÜÇGENLERDE EŞLİK VE BENZERLİKLE İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-1
Aşağıda, TEOG sınavlarında üçgenlerde benzerlik ve eşlik konusuyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2013-2014 TEOG

Şekilde [DE] ⫽ [AB] dir. |CD| = 3 cm, |DE| = 4 cm ve |AB| = 12 cm olduğuna göre, |AD| kaç santimetredir?
Çözüm:

CDE ve CAB üçgenlerinin tepe açıları ortak ve taban açıları yöndeştir. Aynı iç açılara sahip olduğu için CAB ve CDE üçgenleri benzerdir.
CAB ~ CDE
Benzer olan bu üçgenlerin kenar uzunlukları arasındaki ilişki aşağıdaki gibidir.
... ...
Yukarıdaki eşitlikte değeri bilinen kenar uzunlukları yerlerine yazıldığında, |CA|'nın 9 cm'ye eşit olduğu görülebilir.
... ...
⇒ |CA| = 9 cm
|AD| uzunluğu ise, |CA| ile |CD|'nin farkına eşittir.
|AD| = |CA| – |CD| = 9 – 3 = 6 cm
CEVAP: A
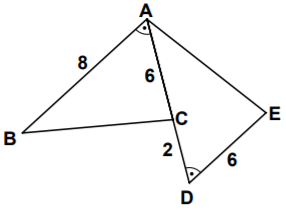
Şekildeki A, C, D noktaları doğrudaş ve ...'tir. |AC| = |DE| = 6 cm, |CD| = 2 cm, |AB| = 8 cm, |BC| = (3x – 2) cm ve |AE| = (2x + 1) cm olduğuna göre, |AE| kaç santimetredir?
Çözüm:
ABC ve DAE üçgenlerinin birer açıları ortaktır. Ayrıca, ortak açıyı oluşturan kenarlar aynı uzunluktadır.
- ...
- |AC| = |DE| = 6 cm
- |AB| = |AD| = 8 cm
Yukarıdaki bilgiler ABC ve DAE üçgenlerinin eş olduğunu gösterir. Buna göre, x cinsinden verilen kenar uzunlukları da eşit olmalıdır.
|BC| = |AE|
⇒ 3x – 2 = 2x + 1
⇒ 3x – 2x = 1 + 2
⇒ x = 3
2x + 1 ifadesinde x yerine 3 yazıldığında, 7 sonucu elde edilir. Bu nedenle |AE| = 7 cm'dir.
CEVAP: C
Bir dik üçgenin hipotenüsü 50 cm'dir. Bu üçgenin dik kenarlarının orta noktalarını birleştiren doğru parçasının uzunluğu kaç santimetredir?
Çözüm:

Yukarıdaki şekilde, bir ABC dik üçgeni ve bu dik üçgenin dik kenarlarının orta noktalarını birleştiren bir [DE] doğru parçası görüyoruz.
ABC ve DBE üçgenlerinin dik açıları ortak ve bu açıyı oluşturan kenar uzunlukları arasındaki oran
... ...'dir.
Buna göre, ABC ve DBE üçgenleri benzerdir. DBE üçgeninin ABC üçgenine benzerlik oranı ...'dir.
|AC| = 50 cm olduğuna göre |DE|'nin uzunluğu ... cm'dir.
CEVAP: D
2014-2015 TEOG

Şekildeki F, G, H ve T noktalarından hangisi [DE]'nın uç noktalarıyla birleştirilirse ABC üçgenine eş bir üçgen elde edilir?
Çözüm:
Bir üçgenin ABC üçgenine eş olabilmesi için tüm kenar uzunluklarının ABC'ninkilerle aynı olması gerekir. [DE] doğru parçası, bu üçgenin kenarlarından biridir ve uzunluğu |AB|'ye eşittir. Buna göre, ABC'ye eş olan üçgenin diğer iki kenar uzunluğu |BC| ve |AC| ile aynı olmalıdır.
|BC| uzunluğu, dik kenarları 1 ve 3 birim olan bir dik üçgenin hipotenüsüne eşittir. Bu mesafe, F ve D noktaları arasındaki uzaklığa eşit olduğu için F noktasının [DE]'nin uç noktaları ile birleştirilmesiyle elde edilen üçgen, ABC'ye eştir.

CEVAP: A

Şekilde [DE] ⫽ [BC] ve [EC] ⫽ [AB]'dir. |AB| = 12 cm, |AD| = 6 cm ve |EC| = 4 cm olduğuna göre, |DC| kaç santimetredir?
Çözüm:
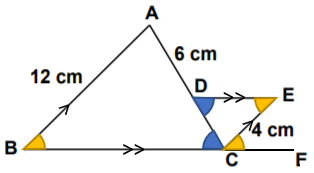
[BC] doğru parçasını sağa doğru uzatalım.
[EC] ⫽ [AB] olduğu için ... ve ... açıları yöndeştir. Ayrıca, [DE] ⫽ [BC] olduğu için ... ile ... iç ters açılardır. Buna göre,
...'dir.
... ve ... açıları iç ters açılardır ve ölçüleri eşittir.
İç açıları aynı olduğu için ABC ve CED üçgenleri benzerdir. CED üçgeninin ABC üçgenine benzerlik oranı
...'tür.
Bu benzerlik oranı, diğer bir eş açının karşısında olan [DC] ve [AC] kenarları arasında da bulunmalıdır. |DC| uzunluğuna x dersek, |AC| uzunluğu 6 + x olur. Bu iki uzunluğu oranlayıp, benzerlik oranına eşitlediğimizde |DC|'nin 3 cm'ye eşit olduğunu görebiliriz.
...
⇒ ...
⇒ ...
⇒ ...
CEVAP: D
