ÇIKMIŞ SORULAR: ÇARPAN NEDİR? ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ

Çarpanlarla ilgili LGS'de (Liselere Giriş Sınavında) çıkan soruları ve bu soruların çözümlerini aşağıda bulabilirsiniz.

LGS'DE ÇIKAN SORU SAYISI
	2017-2018	2018-2019	2019-2020	2020-2021	2021-2022	2022-2023	2023-2024
Soru Sayısı	1	1	1	1	1	1	0

LGS'DE ÇIKAN SORU SAYISI
	Soru Sayısı
2017-2018	1
2018-2019	1
2019-2020	1
2020-2021	1
2021-2022	1
2022-2023	1
2023-2024	0

(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)

2017-2018 LGS

Soru 1: (2017-2018 LGS Sorusu)

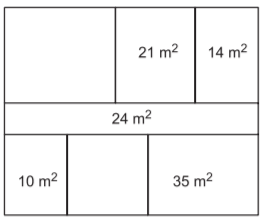
Yukarıdaki her bir bölümü dikdörtgen şeklinde olan dikdörtgen biçimindeki kat planı üzerinde bazı bölümlerin alanları verilmiştir.

Bu dikdörtgenlerin her birinin kenar uzunlukları metre cinsinden birer doğal sayı olduğuna göre alanı verilmeyen bölümlerin alanları toplamı en az kaç metrekaredir?

A) 36

B) 54

C) 64

D) 76

Çözüm:

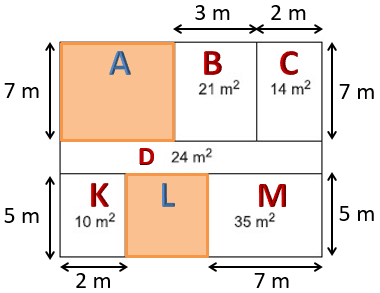
Toplam alanlarını hesaplayacağımız bölümleri turuncu ile gösterelim. Ayrıca, şekli daha rahat takip edebilmek için kat planındaki bölümlere A, B... gibi isimler verelim.

Soruda verilenlere göre, tüm bölgeler dikdörtgen şeklindedir ve kenar uzunlukları doğal sayıdır. Dikdörtgenin alanı kenar uzunluklarının çarpımına eşit olduğu için kat planındaki bir bölümün kenar uzunlukları, alanının çarpanlarıdır. Turuncu bölgelerin toplam alanının alabileceği en küçük değeri hesaplayabilmek için kenar uzunluklarının alabileceği değerleri bulmamız gerekir.

L bölümü:

L'nin solunda ve sağında kalan bölümlerin alanları, sırasıyla, 10 m² ve 35 m²'dir. Bu dikdörtgenlerin genişlik ve yüksekliklerinin alabileceği değerleri bulalım.

Kat planının geometrisinden dolayı, K ve M dikdörtgenlerinin yükseklikleri eşittir. Bu uzunluk, 10 ve 35'in ortak çarpanlarından biri olmalıdır.

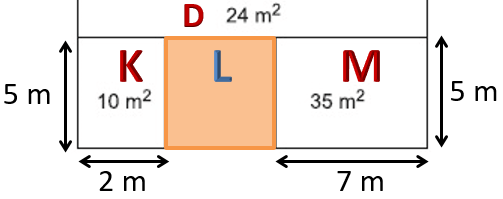
10'un çarpanları 1, 2, 5 ve 10'dir.
35'in çarpanları ise 1, 5, 7 ve 35'dir.

Buna göre K ve M'nin ortak yüksekliği ya 1 m ya da 5 m'dir.

K ve M'nin yükseklikleri 1 m olsaydı, genişlikleri sırasıyla 10 m ve 35 m olurdu. Fakat bu mümkün değildir. Çünkü D'nin genişliği en fazla 24 m olabildiği halde, sadece M'nin genişliği dahi bu değeri aşmaktadır. Ortak çarpanlardan 1'i elediğimizde, geriye bir ortak çarpan kalır: 5. Buna göre, hem K'nın hem de M'nin yüksekliği kesinlikle 5 m'dir. Yan yana gelen dikdörtgenlerin yükseklikleri eşit olduğundan, L'nin yüksekliği de 5 m'dir.

Verilen alanları kullanarak K ve M'nin genişliklerinin metre cinsinden sırasıyla 2 ve 7 olduğunu görebiliriz. Buna göre D'nin genişliği 2 + 7 = 9 m'den uzun olmalıdır. 24'ün 9'dan büyük iki çarpanı bulunmaktadır: 12 ve 24.

D'nin genişliğini 12 m varsaydığımızda, L'nin genişliği 12 – 9 = 3 m olur. D'nin genişliğini 24 m varsaydığımızda ise, L'nin genişliği 24 – 9 = 15 m olur. Toplam alanın en küçük değerini bulmaya çalıştığımız için D'nin genişliğinin 12 m olduğunu varsayabiliriz. Bu durumda L'nin alanı 3 × 5 = 15 m² olur.

(Bir sonraki adımda, A'nın alanını hesaplarken D'nin genişliğin 12 metreden fazla olduğu çıkarsa, bu genişliğin 24 m olduğunu düşünüp, alan hesaplamalarını buna göre tekrarlamamız gerekir.)

A bölümü:

A, B ve C bölümlerinin yükseklikleri eşittir. Ortak yüksekliğin ne kadar olduğunu bulabilmek için önceki kısımda olduğu gibi verilen alanların çarpanlarına bakmamız gerekir.

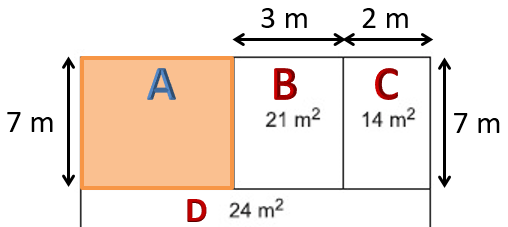
21'in çarpanları 1, 3, 7 ve 21'dir.
14'ün çarpanları ise 1, 2, 7 ve 14'tür.

Ortak çarpanlar 1 ve 7'dir. B ve C'nin yükseklikleri 1 m olamaz çünkü yükseklikleri 1 m olsaydı, genişlikleri sırasıyla 21 m ve 14 m olurdu. Yalnız bu genişliklerin toplamı D'nin tüm çarpanlarından büyüktür. Bu nedenle A, B ve C'nin yükseklikleri 7 m'dir.

Verilen alanları ve bulduğumuz yüksekliği kullanarak B ve C'nin genişliklerinin sırasıyla 3 m ve 2 m olduğunu görebiliriz. L'nin alanını hesaplarken D'nin genişliğinin 12 m olduğunu varsaymıştık. Buna göre A'nın genişliği 12 – (3 + 2) = 7 m'dir. Dolayısıyla, A'nın olası en küçük alanı 7 × 7 = 49 m²'dir.

Toplam Alan

Yukarıdaki çıkarımlara göre, turuncu bölgelerin toplam alanı en az 15 m² + 49 m² = 64 m²'dir.

CEVAP: C

2018-2019 LGS

Soru 2: (2018-2019 LGS Sorusu)

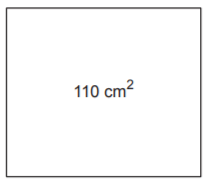
Kenarlarının uzunlukları santimetre cinsinden 1ʼden büyük tam sayı olan dikdörtgen şeklindeki kartonlar ve bu kartonların bir yüzlerinin alanları yukarıda verilmiştir. Bu kartonlardan yüzey alanları farklı olan ikisi seçilip 3 cmʼlik kısımları üst üste yapıştırılarak aşağıdaki gibi bir dikdörtgen karton oluşturulacaktır.

Bu şekilde oluşturulan kartonun bir yüzünün alanı en fazla kaç santimetrekaredir?

A) 91

B) 130

C) 154

D) 187

Çözüm:

Bu kartonlara küçükten büyüğe doğru (soldan sağa doğru) sırayla A, B ve C diyelim.

Soruda verilenlere göre, bir kartonun kenar uzunlukları alanının 1'den büyük çarpanlarıdır. Kartonlara ait kenar uzunluklarının santimetre cinsinden alabileceği değerleri gösteren sayı ikilileri aşağıdaki gibidir.

A kartonu: (5, 7)
B kartonu: (7, 11)
C kartonu: (2, 55) (5, 22) (10, 11)

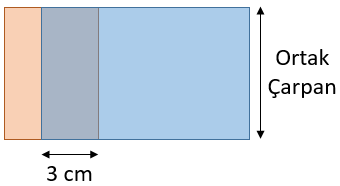
İki farklı karton, şekildeki gibi üst üste yapıştırılacaksa, bu kartonların kenar uzunluklarından biri aynı olmalıdır. Buna göre, olası çözümleri bulabilmek için yukarıdaki ikililerden ortak olanları seçmemiz gerekir. Ortak uzunluğa sahip olabilecek kartonlar ve bu kartonlar yapıştırıldığında oluşan şekillerin alanları aşağıdaki gibidir.

A ve B kartonları

Ortak Uzunluk: 7 cm

Alan = 7 × (11 + 5 – 3) = 91 cm²
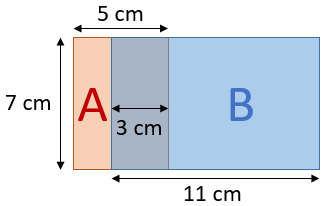
A ve C kartonları

Ortak Uzunluk: 5 cm

Alan = 5 × (7 + 22 – 3) = 130 cm²
B ve C kartonları

Ortak Uzunluk: 11 cm

Alan = 11 × (7 + 10 – 3) = 154 cm²

Olası alanlardan en büyüğü 154 cm²'dir.

CEVAP: C

2019-2020 LGS

Soru 3: (2019-2020 LGS Sorusu)

Yükseklikleri santimetre cinsinden birer tam sayı olan aşağıdaki dikdörtgenler prizması şeklindeki kutuların her birinden üçer adet vardır.

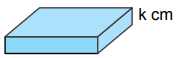
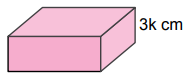
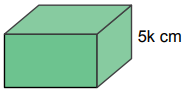
Bu kutular aşağıdaki gibi üst üste dizilerek üç ayrı blok oluşturulmuştur.

Bloklardaki kutuların yerleri değiştirilmeden bu üç blok üst üste konularak bir kule oluşturuluyor. Daha sonra kulenin en üstünde bulunan kutu alınıyor.

Son durumda bu kulenin yüksekliğinin santimetre cinsinden değeri aşağıdakilerden hangisi olamaz?

A) 94

B) 90

C) 86

D) 82

Çözüm:

Kule oluşturulurken 4 çeşit kutunun her birinden 3'er tane kullanılmaktadır. Bu kutuların toplam yüksekliği

3(k + 3k + 5k + 7k) = 3 . 16k = 48k cm'dir.

Sorudaki blokların en üstündeki kutular k, 5k ve 7k yüksekliğindedir. Kule oluşturulurken bloklardan hangisinin en üstte olduğuna bağlı olarak bu kutulardan biri alınmaktadır.

k yüksekliğindeki kutu alınmışsa, kulenin boyu 48k – k = 47k cm,
5k yüksekliğindeki kutu alınmışsa, kulenin boyu 48k – 5k = 43k cm ve
7k yüksekliğindeki kutu alınmışsa, kulenin boyu 48k – 7k = 41k cm'dir.

k bir tam sayı olduğuna göre kulenin yüksekliği 47, 43 veya 41'e tam bölünmektedir. 90, bu sayılardan hiçbirine tam bölünmediği için santimetre cinsinden kulenin yüksekliği olamaz.

CEVAP: B

2020-2021 LGS

Soru 4: (2020-2021 LGS Sorusu)

Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi altı dikdörtgensel bölgeye ayrılmış ve bu bölgelerden bazılarının alanları şekil üzerinde gösterilmiştir.

Elde edilen bu dikdörtgensel bölgelerden her birinin kenarlarının uzunlukları santimetre cinsinden 1'den büyük birer doğal sayıdır.

Buna göre bu kâğıdın bir yüzünün alanı, santimetrekare cinsinden aşağıdakilerden hangisi olabilir?

A) 154

B) 162

C) 180

D) 196

Çözüm:

Soruda verilen birimler temel alındığında dikdörtgensel bölgelerin kenar uzunlukları, alanlarının 1'den büyük çarpanları olur.

35'in çarpanları : 1, 5, 7, 35
21'in çarpanları : 1, 3, 7, 21
44'ün çarpanları : 1, 2, 4, 11, 22, 44
33'ün çarpanları : 1, 3, 11, 33

35 ve 21 sayılarının 1'den büyük tek ortak çarpanı 7'dir. Buna göre, alanı 35 cm² ve 21 cm² olan bölgelerin ortak kenar uzunluğu 7 cm'dir. Bu bölgelere ait diğer kenar uzunlukları ise 35 ÷ 7 = 5 cm ve 21 ÷ 7 = 3 cm'dir.

Benzer şekilde, 44 ve 33'ün 1'den büyük tek ortak çarpanı 11'dir. Dolayısıyla, alanı 44 cm² ve 33 cm² olan bölgelerin ortak kenar uzunluğu 11 cm'dir.

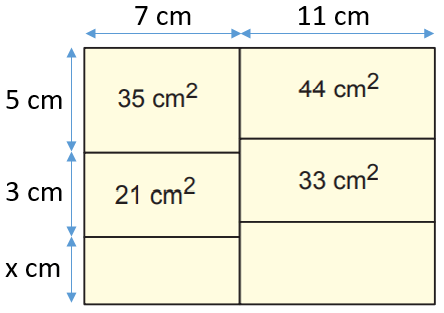
Bulduğumuz kenar uzunluklarını yerlerine yazdığımızda kâğıdın genişliğinin 7 + 11 = 18 cm olduğunu görebiliriz. Ayrıca, sol alttaki bölgenin yüksekliğine x dersek, kâğıdın yüksekliği toplam 8 + x çıkar. x, 1'den büyük bir tam sayı olduğu içi kâğıdın yüksekliği en az 8 + 2 = 10 cm'dir. Buna göre, bir yüzün alanı en az 18 . 10 = 180 cm²'dir.

CEVAP: C

2021-2022 LGS

Soru 5: (2021-2022 LGS Sorusu)

Zeynep'in kalem sayısının çarpanlarından kendisi hariç en büyük iki çarpanı ile Kuzey'in kalem sayısının çarpanlarından kendisi hariç en büyük iki çarpanı aşağıda gösterilmiştir.

Zeynep ve Kuzey, yukarıda verilen çarpanların toplamı kadar kalemi arkadaşlarına vermiştir.

Buna göre, Zeynep ve Kuzey'in toplam kaç kalemi kalmıştır?

A) 22

B) 48

C) 49

D) 64

Çözüm:

Dört veya daha fazla çarpanı olan bir sayının 1 ve kendisi dışındaki çarpanlarından en büyüğü ile en küçüğünün çarpımı bu sayıya eşittir. Örneğin, 24'ün 1 ve 24 dışındaki çarpanları 2, 3, 4, 6 ve 12'dir. Bu çarpanlardan en büyüğü ile en küçüğünün çarpımı 12 × 2 = 24'e eşittir.

Zeynep'in kalem sayısı:

8'e tam bölünen bir sayı 2'ye de tam bölünür. Bu nedenle Zeynep'in kalem sayısının çarpanlarından biri de 2'dir. Bu sayı aynı zamanda 1'den büyük çarpanların en küçüğüdür. Dolayısıyla, Zeynep'in kalemlerinin sayısı 8 × 2 = 16'dır.

Kuzey'in kalem sayısı:

9'a tam bölünen bir sayı 3'e de tam bölünür. 3 sayısı da Kuzey'in kalem sayısının çarpanlarından biridir. Eğer 1'den büyük en küçük çarpan 3'se (2 sayısı çarpanlardan biri değilse) Kuzey'in kalemlerinin sayısı 27 × 3 = 81'dir. 81 sayısının çarpanlarına baktığımızda (1, 3, 9, 27 ve 81) kendisi hariç en büyük iki çarpanının 27 ve 9 olduğunu görüyoruz. Böylece aradığımız Kuzey'in kalem sayısının 81 olduğu sonucuna varabiliriz.

2'nin bir çarpan olup olmadığını test ettiğimizde ise bu sayının 27 × 2 = 54 olması gerektiğini, yalnız bu durumda da 54 hariç en büyük ikinci çarpanın 9 değil 18 olduğunu ve dolayısıyla doğru sayının 54 olmadığını anlayabiliriz.

Özetle, Kuzey'in kalemlerinin sayısı 81'dir.

Kalan kalem sayısı:

Zeynep 8 + 4 = 12 kalemini arkadaşlarına verdiğinde geriye 16 – 12 = 4 kalemi kalır.

Kuzey ise 27 + 9 = 36 kalemini arkadaşlarına verdiğinde geriye 81 – 36 = 45 kalemi kalır.

Geriye kalan toplam kalem sayısı 4 + 45 = 49'dur.

CEVAP: C

→KONU ANLATIMINA DÖN←