BÖLÜM 4: DENKLEMDE SAYIYI VEYA DEĞİŞKENİ KARŞIYA ATMA

Bir eşitliğin iki tarafına da aynı işlemi uyguladığımızda, bu eşitlik bozulmaz. Örneğin, iki tarafa da ... eklediğimizde veya iki tarafı da ...'e böldüğümüzde eşitlik sağlamaya devam eder. Önceki bölümde, denklemleri çözerken iki tarafa da adım adım aynı işlemleri uyguluyorduk.

... ...

⇒ ... ... ...

⇒ ...

Örneğin, bir taraftaki ...'ü yok edebilmek için iki taraftan da ... çıkarıyorduk. Bu işlem sonucunda bir taraftaki ... ile ... birbirini götürüyor ve diğer tarafta fazladan bir ... kalıyordu. Bu işlemi, "bir taraftaki ...'ü diğer tarafa ... olarak atma" şeklinde de yorumlayabiliriz.

⇒ ... ...

⇒ ...

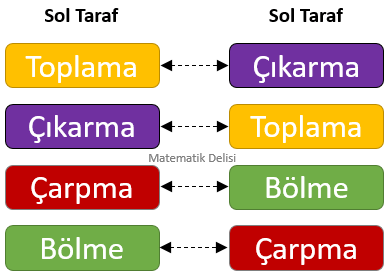
Karşı tarafa atma işlemini yalnız toplama için değil aynı zamanda çarpma, bölme ve çıkarma için de yapabiliriz. Bir terimi veya sayıyı eşitliğin karşı tarafına atarken önceki işlemin tersini uygularız.

Bir tarafta diğer terimlerle toplanan bir terimi, karşı tarafaki terimlerden çıkarırız.
Bir tarafta diğer terimlerden çıkarılan bir terimi, karşı taraftaki terimlerle toplarız.
Bir taraftaki ifadeyi bölen bir sayıyı, karşı taraftaki ifadeyle çarparız.
Bir taraftaki ifadeyle çarpılan bir sayı varsa, karşı taraftaki ifadeyi bu sayıya böleriz.

EŞİTLİĞİN BİR TARAFINDAKİ TERİMİ KARŞI TARAFA ATMA

ÖRNEK:

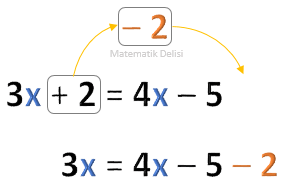
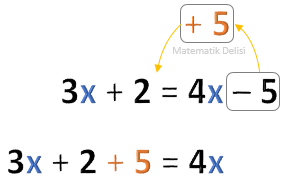
... denklemini çözelim.

...'i sol tarafta yalnız bırakabilmek için ...'yi eşitliğin sağına ... olarak atabiliriz.

⇒ ...

ÖRNEK:

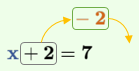
... denklemini çözelim.

Soldaki değişkeni yalnız bırakabilmek için ...'yi karşı tarafa ... olarak geçirebiliriz.

⇒ ...

ÖRNEKLER:

Aşağıdaki denklemlerde kırmızı ile gösterilen terimler eşitliğin karşısına atılmıştır.

... ...

⇒ ... ...
... ...

⇒ ... ...

... ...
⇒ ... ...
... ...

⇒ ... ...

Alıştırmalar-3

Aşağıdaki denklemlerde kırmızı ile gösterilen terimleri eşitliğin karşı tarafına atın.

a) ... ...

b) ... ...

c) ... ...

d) ... ...

e) ... ...

CEVAPLAR

BİR TARAFTAKİ İFADENİN ÇARPANINI KARŞI TARAFA ATMA

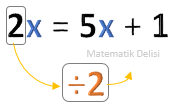
Bir taraftaki tüm terimleri çarpan bir sayı, karşı tarafa atıldığında bu taraftaki tüm terimleri böler.

ÖRNEK:

...

Yukarıdaki denklemde ...'ü karşı tarafa attığımızda hem ...'yi hem de ...'i böler.

⇒ ... ...

ÖRNEK:

... ...

Yukarıdaki denklemde ... sayısı sol taraftaki ifadenin çarpanlarından biridir. Karşı tarafa attığımızda, sağdaki ifadenin tümünü bu sayıya böleriz.

... ...

⇒ ... ...

BİR TARAFTAKİ İFADENİN PAYDASINI KARŞI TARAFA ATMA

Bir taraftaki ifadenin tamamını bölen bir sayı karşı tarafa atıldığında, bu taraftaki tüm terimlerle çarpılır.

ÖRNEK:

... ...

Yukarıdaki denklemin sol tarafındaki ..., bu taraftaki ifadenin tamamını bölmektedir. ...'yi karşı tarafa attığımızda, sağdaki terimlerin tümüyle çarparız.

... ...

⇒ ... ...

ÖRNEKLER:

Aşağıdaki denklemlerde kırmızı ile gösterilen sayılar, eşitliğin karşı tarafına atılmıştır.