ÇIKMIŞ SORULAR: 1. DERECEDEN 1 BİLİNMEYENLİ DENKLEMLERLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-1
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 2 | 3 | 0 | 0 | 1 | 0 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 2 |
| 2018-2019 | 3 |
| 2019-2020 | 0 |
| 2020-2021 | 0 |
| 2021-2022 | 1 |
| 2022-2023 | 0 |
| 2023-2024 | 1 |
Aşağıda, LGS'de 1. dereceden 1 bilinmeyenli denklemlerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2017-2018 LGS
Aşağıdaki tabloda bir lokantada satılan ve her gramında eşit kalori bulunan yemeklerin kütle ve kalorileri verilmiştir.
Tablo: Yemeklerin 100 Gramındaki Kalori Miktarları
| Yemek | Kalori |
| Çorba | 45 |
| Pilav | 72 |
| Nohut | 40 |
Lokantadaki yemekler her bir tabakta 100 gram yemek olacak şekilde satılmaktadır.
Bu lokantadan toplam 538 kalori değerinde 10 tabak yemek sipariş verildiğinde kaç tabak nohut sipariş vermiş olunur?
Çözüm:
Toplam kalori değerinin birler basamağında 8 rakamını görüyoruz. Bu rakamı kullanarak kaç tabak pilav sipariş edildiğini bulabiliriz.

- Nohut'un kalori değeri 10'un tam katıdır. Kaç tabak nohut sipariş edilirse edilsin, nohutlardan toplanan kalori değerinin birler basamağı 0'dır.
- Bir tabak çorbanın kalori değeri 5'in tam katıdır. Bu nedenle, sipariş edilen tabak sayısına göre çorbalardan elde edilen toplam kalori değerinin birler basamağındaki rakam 0 veya 5'tir. Bu rakam 5 olsaydı, pilavlardan elde edilen toplam kalori miktarının birler basamağında 8 – (5 + 0) = 3 rakamının olması gerekirdi. Yalnız, 72 hangi tam sayıyla çarpılırsa çarpılsın, sonucun birler basamağındaki rakam 3 olmaz. Buradan, çorbalardan elde edilen kalori miktarının birler basamağındaki rakamın 0 olduğunu çıkarabiliriz.
- Diğer iki yemeğin toplam kalori değerlerinin birler basamağında 0 rakamı olduğuna göre, pilavların toplam kalori değerinin birler basamağındaki rakam 8'dir.
Pilavların toplam kalori değerinin birler basamağındaki rakam 8'se, sipariş edilen tabak sayısı ya 4 ya da 9'dur. 9 tabak pilav 9 × 72 = 648 kalori yapar. Bu değer soruda verilen toplam kaloriden fazla olduğu için sipariş edilen pilav sayısı 4'tür. Pilavlardan elde edilen toplam kalori değeri ise 4 × 72 = 288'dir.
Geriye kalan 538 – 288 = 250 kalori, 10 – 4 = 6 tabak çorba ve nohuttan elde edilmiştir. Sipariş edilen nohut x tabaksa, çorba 6 – x tabaktır. Buna göre, nohutlardan elde edilen kalori miktarı 40x ve çorbalardan elde edilen kalori miktarı 45(6 – x)'tir. Bu iki sayının toplamı 250'ye eşittir.
40x + 45(6 – x) = 250
⇒ 40x + 270 – 45x = 250
⇒ 270 – 250 = 45x – 40x
⇒ 20 = 5x
⇒ x = 4
CEVAP: C
Bir telefon şirketi müşterilerine fatura ödemelerinde iki indirim seçeneği sunmaktadır.
1. seçenek: Fatura tutarında % 10 indirim
2. seçenek: Fatura tutarında 4 lira indirim
1. seçeneği tercih eden bir müşteri 2. seçeneği tercih etmiş olsaydı 3 lira daha fazla ödeme yapacaktı.
Buna göre bu müşterinin fatura tutarı kaç liradır?
Çözüm:
Bir fiyatta % 10 indirim yapılması, bu fiyatın % 90'ına düşeceği anlamına gelir. % 90'ın kesirli gösterimi ...'dur.
Fatura tutarına x dersek,
- 1. seçeneği tercih eden bir müşteri ... lira ödeme yapar.
- 2. seçeneği tercih eden bir müşteri ise ... lira ödeme yapar.
2. seçenek, 1. seçenekten 3 lira fazlaysa, 1. seçeneğe 3 lira eklediğimizde ödemeler eşitlenir. Matematiksel olarak bunu
... ...
şeklinde ifade edebiliriz. Oluşturduğumuz denklemi çözebilmek için x'li terimleri sol tarafta ve sabit terimleri sağ tarafta toplayalım.
...
Sol ve sağ taraftaki terimler arasındaki işlemleri yapalım.
...
İki tarafı da 10'la çarparsak, fatura tutarının 70 lira olduğunu görebiliriz.
CEVAP: D
2018-2019 LGS
Eşit uzunluktaki iki çubuğun birinden 8 cmʼlik bir parça kesilerek kalan kısım iki eş parçaya, diğerinden 5 cmʼlik bir parça kesilerek kalan kısım üç eş parçaya aşağıdaki gibi ayrılıyor.

Bu parçalardan birer tanesi ile bir kitabın aynı kenarı aşağıdaki gibi ölçüldüğünde parçalardan birinin uzunluğu kitabın kenar uzunluğundan 10 cm fazla, diğerinin uzunluğu ise 1 cm eksik oluyor.

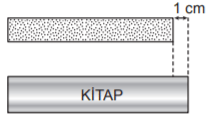
Buna göre kesilmeden önce çubuklardan birinin uzunluğu kaç santimetredir?
Çözüm:
Çubukların uzunluklarını ... ile gösterip, parça uzunluklarını bu değişken cinsinden bulalım.
Üstteki çubuğun parçası:
Üstteki çubuğun 8 cm'si kesilince geriye ... cm'si kalır. Geriye kalan kısım ikiye bölününce, parçalardan her birinin boyu ... cm olur.
Alttaki çubuğun parçası
Alttaki çubuğun 5 cm'si kesilince geriye kalan kısım ... cm uzunluğunda olur. Bu kısım üçe bölününce, parçalardan her biri ... cm uzunluğunda olur.
Şimdi de yukarıda bulduğumuz ifadelerle bir denklem oluşturup, bu denklemi çözelim.
Denklem
Üstteki çubuğun bir parçası soruda verilen kitaptan 10 cm uzun ve alttaki çubuğun bir parçası aynı kitaptan 1 cm kısadır. Buna göre, ...'nin 10 eksiği, ...'ün 1 fazlasına eşittir.
... ...
Denklem Çözümü
Denklemdeki paydalardan kurtulabilmek için eşitliğin iki tarafını da 6 ile çarpabiliriz.
... ...
⇒ ... ... ... ...
⇒ ... ... ... ...
⇒ ... ... ...
⇒ ... ...
⇒ ... ...
⇒ ... cm
CEVAP: B
Yükseklikleri eşit olan dik dairesel silindir şeklindeki iki eş pakete kakaolu ve vanilyalı bisküviler, tabanları çakışacak şekilde aşağıdaki gibi tek sıra hâlinde yerleştiriliyor.

Kakaolu bir bisküvinin yüksekliği vanilyalı bir bisküvinin yüksekliğinin yarısı kadardır. Paketlerden birine üç vanilyalı, iki kakaolu bisküvi konulduğunda paketin boş kalan kısmının yüksekliği 10 cm; diğer pakete bir vanilyalı iki kakaolu bisküvi konulduğunda paketin boş kalan kısmının yüksekliği 14 cm oluyor.
Tam dolu bir paketteki vanilyalı bisküvi sayısı kakaolu bisküvi sayısına eşit olduğuna göre bu pakette kaç tane bisküvi vardır?
Çözüm:
Kakaolu bisküvinin santimetre cinsinden yüksekliğine x dersek, vanilyalı bisküvinin yüksekliği 2x olur. Şimdi de paket yüksekliklerini x cinsinden bulalım.
Soldaki paketin yüksekliği
Soldaki paketin yüksekliği, 3 vanilyalı ve 2 kakaolu bisküvinin toplam yüksekliğinden 10 cm fazladır.
3 . 2x + 2 . x + 10 = 8x + 10 cm
Sağdaki paketin yüksekliği
Sağdaki paketin yüksekliği, 1 vanilyalı ve 2 kakaolu bisküvinin toplam yüksekliğinden 14 cm fazladır.
1 . 2x + 2 . x + 14 = 4x + 14 cm
Denklem
Paketlerin yükseklikleri eşit olduğu için 8x + 10 ile 4x + 14 ifadeleri eşittir.
8x + 10 = 4x + 14
⇒ 8x – 4x = 14 – 10
⇒ 4x = 4
⇒ x = 1 cm
Bisküvilerin ve paketin yükseklikleri
- Vanilyalı bisküvi: 2x = 2 cm
- Kakaolu bisküvi: x = 1 cm
- Paket: 8x + 10 = 18 cm
Tam dolu paketteki bisküvi sayısı
Bir vanilyalı ve bir kakaolu bisküvinin toplam yüksekliği 2 + 1 = 3 cm'dir. Vanilyalı ve kakaolu bisküviler eşit sayıda olacaksa, tam dolu pakette 18 ÷ 3 = 6 çift veya toplam 12 adet bisküvi olmalıdır.
CEVAP: B

Zeynep parasının yarısı ile paketi 30 lira olan A marka ve diğer yarısı ile paketi 50 lira olan B marka kedi mamalarından alıyor. Bu paketlerden markası aynı olan 6 tanesini evinde beslediği kedileri için ayırdıktan sonra kalan paketleri bir hayvan barınağına veriyor.
Zeynep’in hayvan barınağına verdiği A marka ve B marka mamaların paketlerinin sayıları eşit olduğuna göre Zeynep mamalar için toplam kaç lira harcamıştır?
Çözüm:
Zeynep, A ve B marka kedi mamalarına aynı parayı harcadığına göre, ucuz olan A marka mamadan daha fazla almıştır. Markası aynı olan 6 paket mamayı eve bıraktığında kalan paketlerin sayıları eşit olduğundan, eve bıraktığı mamalar A markadır.
B marka kedi mamalarının sayısına x dersek, A marka kedi mamalarının sayısı x + 6 olur. Buna göre, B marka mamalara harcadığı para 50x TL ve A marka mamalara harcadığı para 30(x + 6) TL'dir.
A ve B markalarına aynı parayı verdiği için 50x ile 30(x + 6) ifadeleri eşittir.
50x = 30(x + 6)
⇒ 50x = 30x + 180
⇒ 50x – 30x = 180
⇒ 20x = 180
⇒ x = 9
x = 9 ise, Zeynep'in B marka mamaya verdiği para 50 . 9 = 450 TL'dir. Bu miktar, harcadığı paranın yarısı olduğu için doğru cevap 450 . 2 = 900 TL'dir.
CEVAP: D
