BÖLÜM 2: DEĞİŞKENLERLE TEMEL İŞLEMLER

Bu bölümde değişkenler ve sabit sayılar arasında yapılan toplama, çıkarma, çarpma ve bölme işlemleri üzerine yoğunlaşıyoruz.

DEĞİŞKENLERDE TOPLAMA VE ÇIKARMA

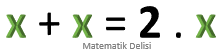
a tane değişkenin toplamı, a ile bu değişkenin çarpımına eşittir. Örneğin, 7 tane x'in toplamı 7 . x'e ve 13 tane y'nin toplamı 13 . y'ye eşittir.

ÖRNEKLER:

x + x = 2 . x
y + y + y = 3 . y
z + z + z + z = 4 . z
t + t + t + t + t = 5 . t

Aynı değişkenlerin ve sabit sayıların toplandığı işlemlerde, değişkenleri kendi aralarında ve sabit sayıları kendi aralarında toplarız.

ÖRNEKLER:

x + x + 3 + 5 = 2 . x + 8
7 + y + 3 + y – 2 + y = 3 . y + 8
z – 5 – 10 = z – 15
–5 + t + 3 + t + t = 3 . t – 2

Bir değişkeni kendisinden çıkardığımızda sonuç 0 olur.

ÖRNEKLER:

a – a = 0
x + 5 – x = 5
y + 2 – y + 5 – y + y = 7
z – z + z + 2 = z + 2

DEĞİŞKENLERDE ÇARPMA

Bir sabit sayıyla değişkenin çerpımını gösterirken aradaki "×" veya "." işaretini kaldırabiliriz. Örneğin, 3 ile y'nin çarpımını "3 × y" veya "3 . y" yerine "3y" şeklinde gösterebiliriz.

Bir sabit sayıyla değişkeni çarparken, sabit sayıların çarpımındaki kuralları kullanırız.

ÖRNEK:

3 . x = 3x
5 . a = 5a
(–2) . x = –2x
0 . y = 0
(–5) . (–x) = 5x

Sabit sayılarda olduğu gibi, bir değişkeni kendisi ile çarpımı, tabanı bu değişken olan üslü bir sayıya eşittir.

ÖRNEK:

x . x = x²
(–a) . (–a) = (–a)² = a²
x . x . x = x³
y . y . y . y = y⁴

Farklı değişkenleri de birbiri ile çarpabiliriz.

ÖRNEK:

x . y = xy
a . b . c = abc
x . x . y = x²y

DEĞİŞKENLERDE BÖLME

Bir bölme işleminde

Yalnız bölenin değişken olduğu,
Yalnız bölünenin değişken olduğu veya
Hem bölen hem de bölünenin değişken olduğu

durumlarla karşılaşabiliriz. 0'a bölme işlemi tanımsız olduğu için bölenin değişken olduğu durumlarda, bu değişkenin 0 değerini alamayacağına dikkat etmemiz gerekir.

ÖRNEK: