ÇIKMIŞ SORULAR: CEBİRSEL İFADELERLE İŞLEMLERLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-2
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 1 | 1 | 1 | 0 | 1 | 4 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 1 |
| 2018-2019 | 1 |
| 2019-2020 | 1 |
| 2020-2021 | 0 |
| 2021-2022 | 1 |
| 2022-2023 | 4 |
| 2023-2024 | 1 |
Aşağıda, LGS'de cebirsel ifadelerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki sayfaya geçebilirsiniz.
Alanı (36x2) cm2 olan kare, alanları birbirine eşit olan mavi, sarı ve beyaz renkli üç dikdörtgensel bölgeye aşağıdaki gibi ayrılmıştır.
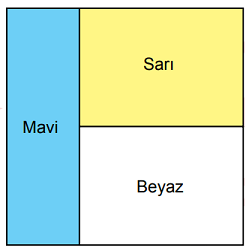
Buna göre, sarı dikdörtgensel bölgenin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
36x2 = 6x · 6x olduğundan, karenin kenar uzunluğu 6x cm'dir. Mavi, sarı ve beyaz dikdörtgenlerin alanları eşit ve bu alanların toplamı (36x2) cm2'dir. Buna göre dikdörtgenlerden her birinin alanı (36x2) ÷ 3 = (12x2) cm2'dir.
Verilen şekle göre, sarı ve beyaz dikdörtgenlerin genişlikleri eşittir. Alanları da eşit olan bu dikdörtgenlerin yükseklikleri de eşit olmalıdır. Bu yükseklik, karenin kenar uzunluğunun yarısıdır.
(6x) ÷ 2 = (3x) cm
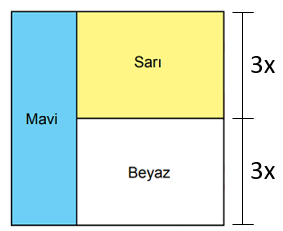
Alanı (12x2) cm2 ve yüksekliği (3x) cm olan sarı dikdörtgenin genişliği (12x2) ÷ (3x) = (4x) cm'dir.
Genişliği (4x) cm ve yüksekliği (3x) cm olduğu için sarı dikdörtgenin çevresi 2(4x + 3x) = 14x cm'dir.
CEVAP: C
Dikdörtgen biçimindeki bir kâğıt, Şekil I'deki gibi kesiliyor. Daha sonra elde edilen parçaların kenarları Şekil II'deki gibi çakıştırılarak bir yüzünün alanı (16x2) cm2 olan, kare şeklinde bir kağıt elde ediliyor.

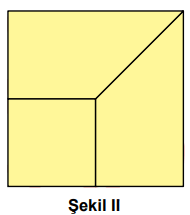
Buna göre, başlangıçta verilen dikdörtgen şeklindeki kâğıdın çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
16x2 = 4x · 4x olduğundan Şekil II'deki karenin kenar uzunluğu 4x cm'dir.

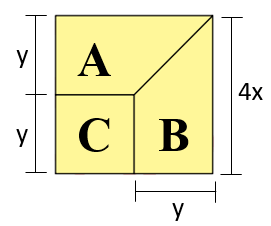
Şekil I'deki dikdörtgenin yüksekliğini y ile ifade edip, bu yüksekliği şekil II'de ilgili yerlere yazarsak C'nin bir kare olduğunu görebiliriz.
2y = 4x olduğundan y = 2x'tir. Buna göre, C karesinin kenar uzunluğu (2x) cm; A ve B yamuklarının kısa tabanları (2x) cm, uzun tabanları (4x) cm ve yükseklikleri (2x) cm uzunluğundadır.


Bulduğumuz uzunlukları yerlerine yazarak şekil I'deki dikdörtgenin çevresinin (20x) cm olduğunu görebiliriz.
4x + 2x + 2x + 2x + 2x + 4x + 2x + 2x = 20x cm
CEVAP: B
Dokuz eş kareden oluşan kare, Şekil I'de; dört eş dikdörtgenden oluşan dikdörtgen, Şekil II'de verilmiştir. Bu şekillerin yükseklikleri birbirine eşittir.
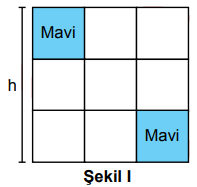
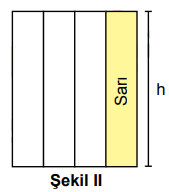
Şekil I'de verilen mavi bölgelerin alanları toplamı, Şekil II'de verilen sarı bölgenin alanına eşittir.
Şekil I'in çevresinin uzunluğu (36x + 36) cm olduğuna göre, Şekil II'nin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
Mavi karenin kenar uzunluğu, h yüksekliğinin 3'te 1'idir.
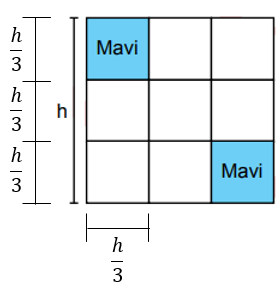
Alanı ise, bu uzunluğun karesidir.
Mavi karenin alanı = ...
İki mavi karenin toplam alanını bulabilmek için yukarıdaki ifadeyi 2'yle çarparız.
Mavi karelerin toplam alanı = ...
Sarı bölgenin tabanına y dersek, alanı y · h = olur. Bu değer, mavi karelerin toplam alanına eşittir.
...
⇒ ...
Buna göre, sarı bölgenin tabanı ...'dur.
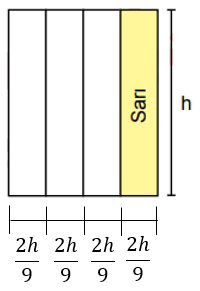
II. şeklin taban uzunluğu
...'dur.
Çevre uzunluğunu h cinsinden aşağıdaki gibi hesaplayabiliriz.
Çevre = ...
h uzunluğu, ilk şeklin çevresinin 4'te 1'idir.
... ...
Çevre için bulduğumuz ... ifadesinde ... yerine ... yazarak sonuca ulaşabiliriz.
Çevre = ... ...
CEVAP: A
2023-2024 LGS
Bir kenar uzunluğu (x + 2) cm olan karenin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
Karenin çevre uzunluğu, kenar uzunluğunun 4 katıdır. Kenar uzunluğu için verilen ifadeyi 4'le çarptığımızda
4 · (x + 2)
ifadesini elde ederiz. Çarpmanın toplama üzerine dağılma özelliğini kullanarak doğru yanıtın D seçeneği olduğunu görebiliriz.
4 · (x + 2) = 4 · x + 4 · 2
= 4x + 8
CEVAP: D
