ÇIKMIŞ SORULAR: ÖZDEŞLİKLERLE İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-1

Aşağıda, TEOG sınavlarında özdeşliklerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.

2013-2014 TEOG

Soru 1: (2013-2014 TEOG 2. Dönem Sınav Sorusu)

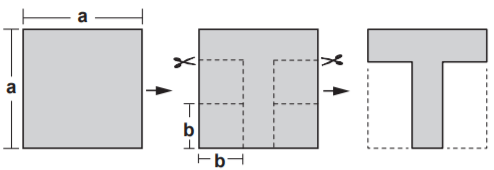
Bir kenarının uzunluğu a birim olan kare şeklindeki bir kağıttan, bir kenarının uzunluğu b birim olan kare şeklinde dört eşit parça yukarıdaki gibi kesilip çıkarılıyor. Kalan kağıdın bir yüzünün alanının kaç birimkare olduğunu gösteren cebirsel ifade aşağıdakilerden hangisi ile özdeştir?

A) (a – 4b)²

B) (a – 2b)²

C) (a – 4b)(a + 4b)

D) (a – 2b)(a + 2b)

Çözüm:

Karenin alanı bir kenar uzunluğunun karesine eşittir.

Kağıdın kesilmeden önceki alanı a² ve kesilen her bir parçanın alanı b²'dir. Kağıttan toplam 4 parça kesildiği için kesilen toplam alan 4b²'dir. Buna göre geriye kalan kağıdın alanı a² – 4b²'dir.

a² – 4b² ifadesi (a – 2b)(a + 2b) ile özdeştir.

CEVAP: D

Soru 2: (2013-2014 TEOG 2. Dönem Mazeret Sınavı Sorusu)

Aşağıdakilerden hangisi bir özdeşliktir?

A) 2(d – 4) = –8 + 2d

B) 3(y – 4) = 12 – 3y

C) 20 + 4c = 5(4 + c)

D) 5x + 3 = 5(x + 3)

Çözüm:

Bir denklemin özdeşlik olabilmesi için değişkenin değerinden bağımsız olarak, eşitliğin iki tarafının birbirine eşit olması gerekir.

A) Sol taraftaki parantezi açtığımızda, 2d – 8 ifadesini elde ederiz. Bu ifadede 2d ile –8'in yerini değiştirdiğimizde, eşitliğin sağındaki –8 + 2d ifadesini elde ederiz. Bu seçenekteki eşitlik bir ÖZDEŞLİKTİR.

B) Soldaki parantezi açarsak, 3y – 12 ifadesini elde ederiz. Yalnız bu ifade eşitliğin sağ tarafındaki ifade ile aynı değildir. Bu nedenle B seçeneğindeki eşitlik bir ÖZDEŞLİK DEĞİLDİR.

C) Sağdaki parantezi açtığımızda, 20 + 5c ifadesi ile karşılaşırız. Bu ifade, eşitliğin sol tarafındaki ifadeden farklıdır. Verilen eşitlik bir ÖZDEŞLİK DEĞİLDİR.

D) Sağdaki parantezi açtığımızda, 5x + 15 ifadesini buluruz. Bu ifade eşitliğin sol tarafındaki ifadeden farklıdır. Verilen eşitlik bir ÖZDEŞLİK DEĞİLDİR.

CEVAP: A

2014-2015 TEOG

Soru 3: (2014-2015 TEOG 2. Dönem Sınav Sorusu)

Aşağıdakilerden hangisi bir özdeşlik değildir?

A) 2 . (x – 3) = 3 . (x – 2)

B) (x – 3)² = x² – 6x + 9

C) x² – x = x . (x – 2)

D) x² – 4 = (x – 2) . (x + 2)

Çözüm:

A) Eşitliğin sol ve sağ tarafındaki parantezleri açalım.

Eşitliğin sol tarafı: 2 . (x – 3) = 2x – 6
Eşitliğin sağ tarafı: 3 . (x – 2) = 3x – 6

Sol ve sağ taraftaki x'lerin katsayıları aynı olmadığı için A seçeneğinde verilen eşitlik bir özdeşlik değildir.

CEVAP: A

Soru 4: (2014-2015 TEOG 2. Dönem Mazeret Sınavı Sorusu)

Alanı a² metrekare olan arsaya alanı b² metrekare olan bir ev yapılıyor.

a ve b'nin alabileceği her değer için arsanın kalan kısmının alanını gösteren cebirsel ifade aşağıdakilerden hangisidir?

A) (a – b)²

B) 4 . (a – b)²

C) (a – b) . (a + b)

D) 4 . (a – b) . (a + b)

Çözüm:

Soruda verilenlere göre arsanın alanı a² ve evin alanı b²'dir.

Arsanın alanından evin alanını çıkarırsak geriye kalan alanı bulabiliriz. İstenilen alan a² – b²'dir.

a² – b² = (a + b)(a – b)

olduğunu için cevap C'dir.

CEVAP: C

2015-2016 TEOG

Soru 5: (2015-2016 TEOG 1. Dönem Sınav Sorusu)

2x(3x – 5) = 6x² – ax

ifadesi bir özdeşlik olduğuna göre a kaçtır?

A) –5

B) –3

C) 7

D) 10

Çözüm:

Verilen eşitlik bir özdeşlikse eşitliğin sol ve sağ taraflarındaki ifadelerin aynı olması gerekir. Sol taraftaki parantezi açtığımızda 6x² – 10x ifadesini elde ederiz.

2x(3x – 5) = 2x . 3x – 2x . 5 = 6x² – 10x

Buna göre, a = 10'dur.

CEVAP: D

→KONU ANASAYFASINA DÖN←