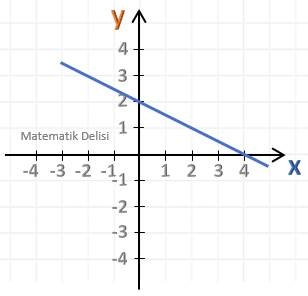BÖLÜM 3: GRAFİKTEN DOĞRUNUN EĞİMİNİ BULMA
Bir doğrunun koordinat sistemindeki grafiğini kullanarak, eğimini bulabilmek için
- Doğru üzerinde iki nokta belirleriz. Bu noktalar A(
x1 ,y1 ) ve B(x2 ,y2 ) olsun. y2 –y1 farkınınx2 –x1 farkına oranı, doğrunun eğimine eşittir.
...
Eğimi hesaplarken seçtiğimiz noktaların x ve y koordinatlarını kullanıyoruz. Bu nedenle
koordinatlarını grafikten net olarak anlayabildiğimiz noktaları seçmemiz önemlidir.
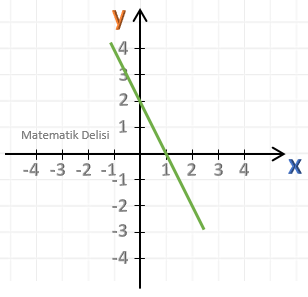
Yukarıdaki doğrunun eğimini bulalım.
Hesaplama yapabilmek için doğru üzerindeki A(
...
Yaptığımız çıkarma işlemlerinde, eksilenler aynı noktaya ait olduğu sürece, seçtiğimiz iki noktadan hangisinin koordinatlarını, hangisinden çıkardığımız farketmez. Örneğin yukarıdaki hesaplamada B noktasının koordinatlarını A noktasınınkilerden çıkarsak da aynı sonucu elde ederiz.
...
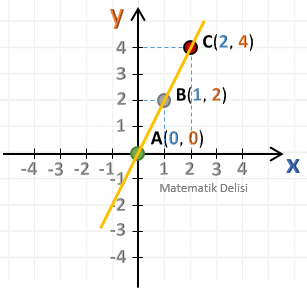
Eğim hesaplarken, koordinatlarını bildiğimiz sürece, hangi iki noktayı seçtiğimiz farketmez. Örneğin, A ve C noktalarını seçtiğimizde de;
B ve C noktalarını seçtiğimizde de
...
...
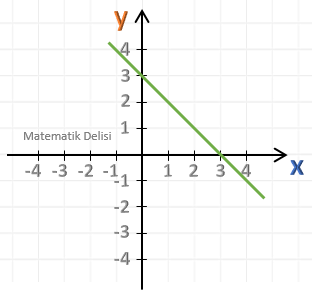
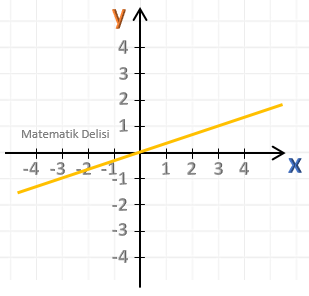
Yukarıdaki doğrunun eğimini bulalım.
Soruda verilen doğru A(
...
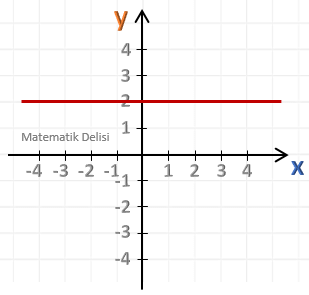
Yukarıdaki doğrunun eğimini bulalım.
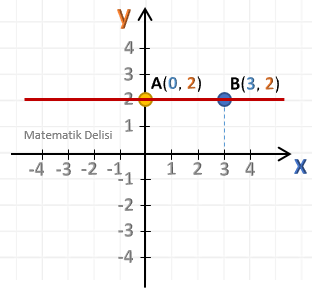
Bu doğru A(
...
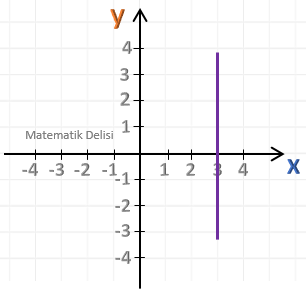
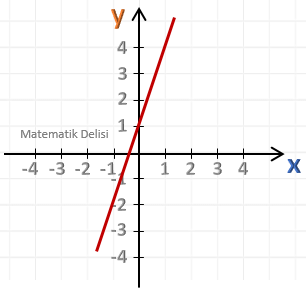
Yukarıdaki doğrunun eğimini bulalım.
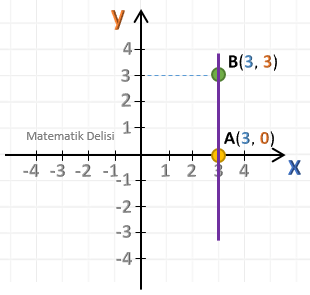
A(
...
