---

NEDEN: ax + by + c = 0 DENKLEMİNİN EKSENLERİ KESTİĞİ NOKTALAR

NEDEN?

Doğrusal denklemlerin grafikleri doğru şeklindedir ve koordinat sisteminde iki farklı noktadan geçen tek bir doğru vardır. Doğru üzerindeki her nokta, denklemin bir çözümü olduğundan denklemdeki eşitliği sağlayan iki farklı sıralı ikili bulmamız, doğrusal denklemin grafiğini çıkarabilmemiz için yeterlidir.

Doğrusal bir denklemin çözümlerinden birini bulabilmek için değişkenlerden birinin yerine bir sayı yazıp, denklemi diğer değişken için çözebiliriz. Denklemde x veya y yerine 0 yazdığımızda, diğer değişkenin değerini kolaylıkla bulabiliriz. Buna göre, a, b ve c sıfırdan farklı olmak üzere, ax + by + c = 0 denkleminde sırasıyla x ve y yerine 0 yazarak denkleme ait grafiğin geçtiği noktaları elde edebiliriz. y = 0 için bulduğumuz çözüm x-ekseninde ve x = 0 için bulduğumuz çözüm y-eksenindedir. Aşağıda bu noktaların koordinatlarını buluyoruz.

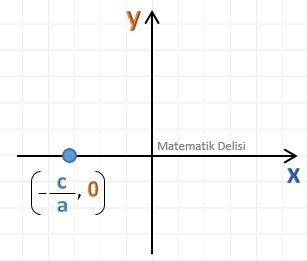
ax + by + c = 0 doğrusunun x-eksenini kestiği nokta

Denklemde y yerine 0 yazıp, x'in değerini bulalım.

...

⇒ ...

⇒ ...

⇒ ...

Buna göre, doğrunun x-eksenini kestiği nokta ...'dır.

ax + by + c = 0 doğrusunun y-eksenini kestiği nokta

Denklemde x yerine 0 yazıp, y'nin değerini bulalım.

...

⇒ ...

⇒ ...

⇒ ...

Dolayısıyla, doğrunun y-eksenini kestiği nokta ...'dir.

Doğrunun Grafiği

Yukarıda bulduğumuz noktalardan geçen doğru, a, b ve c sıfırdan farklı olmak üzere, ax + by + c = 0 denkleminin grafiğidir.

→KONU ANASAYFASINA DÖN←