DÖNÜŞÜM GEOMETRİSİ
DÖNME HAREKETİ
BÖLÜM 2-ŞEKLİN DÖNDÜRÜLMESİ
BU KONU 2018-2019 8. SINIF MATEMATİK KAZANIMLARI ARASINDA BULUNMAMAKTADIR
![]() Bir şeklin döndürülmesi ile üzerindeki tüm
noktaların döndürülmesi aynı şeydir. Bu nedenle şekil
üzerinde bazı noktalar belirleyip, bu noktaları döndürerek,
şeklin yeni pozisyonunu bulabiliriz.
Bir şeklin döndürülmesi ile üzerindeki tüm
noktaların döndürülmesi aynı şeydir. Bu nedenle şekil
üzerinde bazı noktalar belirleyip, bu noktaları döndürerek,
şeklin yeni pozisyonunu bulabiliriz.
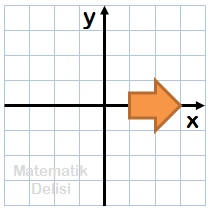
Yukarıdaki şeklin saat yönünde ve tersi yönde 90⁰, 180⁰ ve 270⁰ döndürülmesi sonucunda oluşan şekilleri bulalım.
Şeklin döndürüldüğünde hangi konuma geleceğini bulabilmek için bu şeklin üzerindeki bazı noktaları referans olarak seçip, bu noktaları döndürebiliriz. Biz bu örnekte, şeklin dış çerçevesinin x-ekseni ile kesiştiği iki noktayı seçiyoruz.
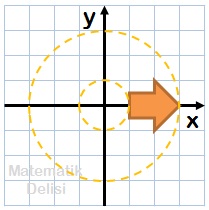
Belirlediğimiz noktalardan geçen orijin merkezli çemberler yukarıda çizilmiştir. Şekil döndürülürken, belirlediğimiz noktaların hareketleri, bu çemberler üzerinde olacaktır. Çemberleri ve referans noktalarını kullanarak, şeklin hagi konumlara gelebileceğini görebiliyorsak, saat yönünde ve tersinde 90⁰, 180⁰ ve 270⁰ derece döndürmeler sonucunda aşağıdaki yeşil, mor ve mavi şekilleri elde edebiliriz.
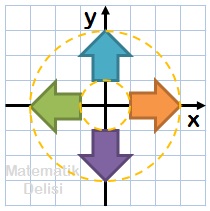
Turuncu okun saat yönünde
- 90⁰ döndürülmesiyle mor ok,
- 180⁰ döndürülmesiyle yeşil ok ve
- 270⁰ döndürülmesiyle mavi ok
elde edilir.
Ayrıca, aynı şeklin saat yönünün tersine
- 90⁰ döndürülmesiyle mavi ok,
- 180⁰ döndürülmesiyle yeşil ok ve
- 270⁰ döndürülmesiyle mor ok
elde edilir.
Çember çizmek ve belirlediğimiz noktaların hangi koordinatlara geleceğini çember yardımıyla bulmak istemiyorsak, bir önceki bölümde öğrendiğimiz kuralları kullanarak da noktaların yeni konumlarını bulabiliriz.
Bu örnek için belirlediğimiz noktaların koordinatları (1, 0) ve (3, 0)'dır.
Bu noktaların saat yönünde
- 90⁰ döndürülmesiyle, sırasıyla, (0, -1) ve (0, -3) koordinatları,
- 180⁰ döndürülmesiyle , sırasıyla, (-1, 0) ve (-3, 0) koordinatları ve
- 270⁰ döndürülmesiyle , sırasıyla, (0, 1) ve (0, 3) koordinatları
elde edilir.
Benzer şekilde (1, 0) ve (3, 0) noktalarının saat yönünün tersine
- 90⁰ döndürülmesiyle, sırasıyla, (0, 1) ve (0, 3) koordinatları,
- 180⁰ döndürülmesiyle , sırasıyla, (-1, 0) ve (-3, 0) koordinatları ve
- 270⁰ döndürülmesiyle , sırasıyla, (0, -1) ve (0, -3) koordinatları
elde edilir.
Şekli, yeni bulduğumuz noktalar arasına yerleştirdiğimizde de yine yuarıda elde ettiğimiz sonuçlara ulaşabiliriz.
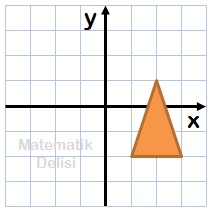
Yukarıdaki şeklin saat yönünde ve tersi yönde 90⁰, 180⁰ ve 270⁰ döndürülmesi sonucunda oluşan şekilleri bulalım.
Turuncu üçgenin saat yönünde
- 90⁰ döndürülmesiyle mor üçgen,
- 180⁰ döndürülmesiyle yeşil üçgen ve
- 270⁰ döndürülmesiyle mavi üçgen
elde edilir.
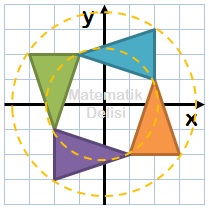
Ayrıca, turuncu üçgenin saat yönünün tersine
- 90⁰ döndürülmesiyle mavi üçgen,
- 180⁰ döndürülmesiyle yeşil üçgen ve
- 270⁰ döndürülmesiyle mor üçgen
elde edilir.
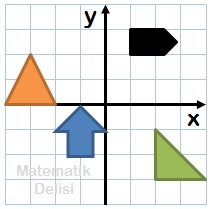
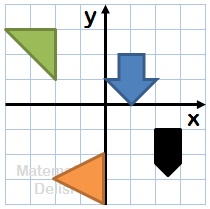
Yukarıdaki şekillerin, verilen yön ve açılarda orijin etrafında döndürülmeleri sonucunda koordinat sisteminde gelecekleri konumları bulalım.
a) Mavi şekil: 180⁰, saat yönünde
b) Turuncu şekil: 90⁰, saat yönünün tersine
c) Siyah şekil: 270⁰, saat yönünün tersine
d) Yeşil şekil: 180⁰, saat yönünün tersine
DÖNÜŞÜM GEOMETRİSİ-ŞEKİL-EĞİTİM ARACI
ÖTELEME HAREKETİ
DÖNME HAREKETİ
YANSIMA HAREKETİ
Bu eğitim aracını yeni pencerede açmak ve nasıl kullanıldığını öğrenmek için tıklayın
KONU ANLATIMLARI
ÇIKMIŞ SORULAR VE ÇÖZÜMLERİ
DÖNME HAREKETİ İLE İLGİLİ ÇIKMIŞ SORULAR VE ÇÖZÜMLERİ