BÖLÜM 2: ŞEKLİN YANSIMASI
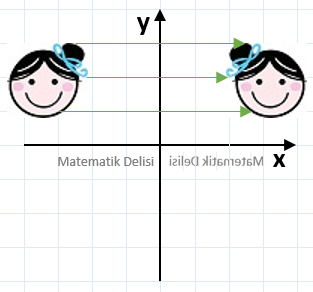
Bir şeklin yansıması, üzerindeki tüm noktaların bu eksene göre yansımasına denktir.
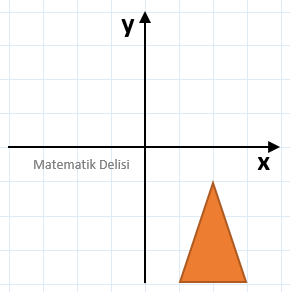
Yukarıdaki üçgenin x-eksenine göre yansımasını bulalım.
Yukarıdaki üçgene ait köşelerin koordinatları (2, –1), (1, –4) ve (3, –4)'tür. Bu noktaların, x-eksenine göre yansımaları sırasıyla (2, 1), (1, 4) ve (3, 4)'tür. Elde edilen noktaların birleştirilmesiyle ortaya çıkan üçgen, soruda gösterilen üçgenin x-eksenine göre yansımasıdır.
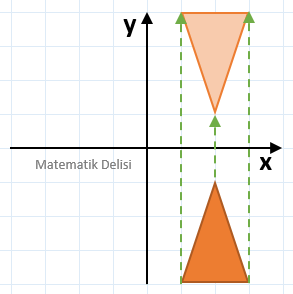
Yukarıdaki üçgenin x-eksenine göre yansımasını bulalım.
Şekildeki üçgenin köşe noktaları (2, 2), (1, –1) ve (3, –1)'dir. Bu noktaların x-eksenine göre yansımaları sırasıyla (2, –2), (1, 1) ve (3, 1) koordinatlarındadır. Elde edilen noktaların birleştirilmesiyle ortaya çıkan şekil aşağıdaki gibidir.
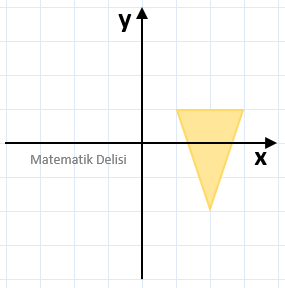
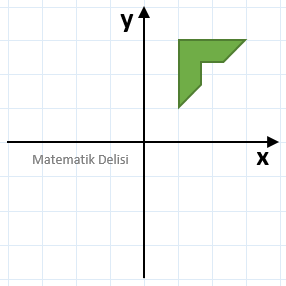
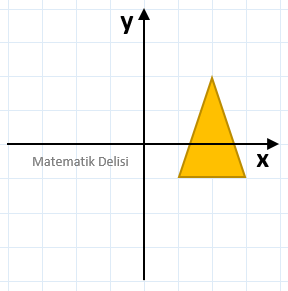
Yukarıdaki şeklin y-eksenine göre yansımasını bulalım.
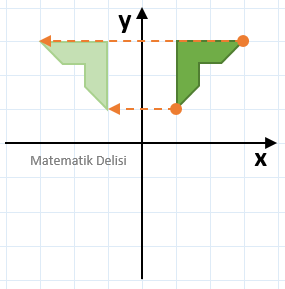
Şekil üzerinde bazı noktalar belirleyip, bu noktaların yansımasını alarak, şeklin hangi pozisyona geleceğini bulabiliriz. Şekil üzerindeki (3, 3) ve (1, 1) noktalarını y-eksenine göre yansımaları sırasıyla (–3, 3) ve (–1, 1)'dir. Bu noktaları referans alarak yansımanın aşağıdaki gibi olduğunu görebiliriz.
Aşağıdaki aracı kullanarak yansıma hareketinin şekil üzerindeki etkilerini görebilirsiniz.
