ÇIKMIŞ SORULAR: EBOB-EKOK PROBLEMLERİYLE İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ

Aşağıda, EBOB-EKOK problemleriyle ilgili çıkan TEOG sorularını ve bu soruların çözümlerini bulabilirsiniz.

(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)

2016-2017 TEOG

Soru 1: (2016-2017 TEOG 1.Dönem Sınav Sorusu)

Bir merdivenin basamakları üçer üçer veya dörder dörder inildiğinde her seferinde 1 basamak artıyor.

Buna göre bu merdiven en az kaç basamaklıdır?

A) 11

B) 13

C) 23

D) 25

Çözüm:

Basamak sayısı, şu ankinden 1 tane az olsaydı, hem 3'ün hem de 4'ün tam katı olurdu. 3 ve 4'ün ortak katlarından en küçüğü 12'dir.

EKOK(3, 4) = 12

Buna göre, merdivendeki basamak sayısı en az 12 + 1 = 13'tür.

CEVAP: B

Soru 2: (2016-2017 TEOG 1.Dönem Mazeret Sınavı Sorusu)

12 ve 18 sayılarına bölündüğünde 5 kalanını veren üç basamaklı en küçük doğal sayı kaçtır?

A) 103

B) 113

C) 115

D) 125

Çözüm:

Yol 1:

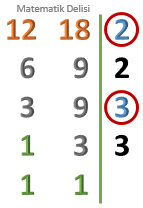
12'ye ve 18'e bölündüğünde 5 kalanını veren bir sayıdan 5 çıkarırsak, bulduğumuz sonuç hem 12'nin hem de 18'in tam katı olur. 12 ve 18'in tam katlarının tümü EKOK(12, 18)'in tam katıdır.

EKOK(12, 18) = 2 . 2 . 3 . 3 = 36'dır ve 36'nın tam katları 36, 72, 108, 144, ...'tür.

36'nın tam katlarına 5 ekleyerek 12 ve 18'e bölündüğünde 5 kalanını veren sayılar elde edebiliriz. Bu sayılar 41, 77, 113, 149, ...'dur. Sorudaki şartlara uyan en küçük 3 basamaklı sayı 113'tür.

Yol 2:

En küçük sayıdan başlayarak, verilen seçenekleri 12 ve 18'e bölüp, kalanın 5'e eşit olup olmadığına bakabiliriz.

A) 103, 12'ye bölündüğünde kalan 7 olur. Bu seçeneği eleyebiliriz.

B) 113, hem 12'ye hem de 18'e bölündüğünde kalan 5 olur.

Diğer seçeneklerdeki sayılar daha büyük olduğu için bu sayıları denememiz gerekmez.

CEVAP: B

→KONU ANASAYFASINA DÖN←