BÖLÜM 2: ASAL ÇARPANLARA AYIRARAK EKOK HESAPLAMA

Verilen sayıların katlarını sıralayıp ortak katlarından en küçüğünü aramak yerine bu sayıları asal çarpanlarına ayırarak da EKOK'u hesaplayabiliriz.

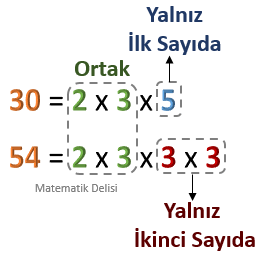
İki sayıyı asal çarpanlarına ayırdığımızda üç grup asal çarpanla karşılaşırız.

Sayıların ikisinde de olan ortak çarpanlar,
İlk sayıda olan ama ikinci sayıda olmayan asal çarpanlar ve
İlk sayıda olmadığı halde ikinci sayıda olan asal çarpanlar.

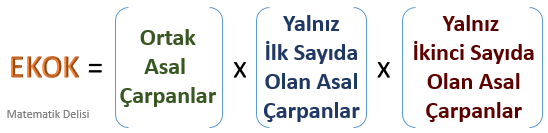
Bu üç kategoride bulunan asal çarpanların tümünü birbiri ile çarptığımızda, verilen sayıların EKOK'unu elde ederiz. Başka bir deyişle, EKOK'u bulabilmek için ortak asal çarpanları çarpma işleminde yalnız bir kere kullanarak, verilen sayıların asal çarpanlarını çarparız.

ÖRNEK:

12 ile 30'un EKOK'unu hesaplayalım.

12 ve 30 sayıları asal çarpanlarına aşağıdaki gibi ayrılır.

Ortak asal çarpanlar: 2 ve 3
12'de olup 30'da olmayan asal çarpanlar: 2
30'da olup 12'de olmayan asal çarpanlar: 5

12 ile 30'un EKOK'u, yukarıda sıraladığımız asal çarpanların çarpımına eşittir.

EKOK(12, 30) = 2 × 3 × 2 × 5 = 60

ÖRNEK:

6 ile 12'nin EKOK'unu hesaplayalım.

6 ve 12 sayılarını asal çarpanlarına aşağıdaki gibi ayırabiliriz.

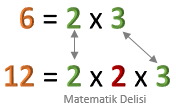
6'nın tüm asal çarpanları aynı zamanda 12'nin de asal çarpanıdır. 6'nın 12'den farklı asal çarpanı yoktur. 12'nin 6'dan farklı tek asal çarpanı 2'dir. Ortak çarpanlarla 2'yi çarparak verilen sayıların EKOK'unu bulabiliriz.

EKOK(6, 12) = 2 × 3 × 2 = 12

Alıştırmalar-1

Aşağıdaki sayıların EKOK'larını hesaplayın.

a) 24 ile 12, b) 30 ile 12, c) 36 ile 28, d) 35 ile 180, e) 90 ile 220, f) 4 ile 20

CEVAPLAR

ASAL ÇARPANLARLA EKOK HESAPLAMA ARACI
👉🏻EKOK hesaplama aracı-Tıklayın👈🏻

Üslü gösterim kullanıldığında, EKOK'u hesaplayabilmek için yalnız ortak olanları değil, tüm tabanları yazar, kuvvetlerden büyük olanları seçeriz. Ortaya çıkan çarpma işleminin sonucu EKOK'u verir.

ÖRNEK:

2 . 3² . 5³ ile 3⁴ . 5 . 7³ sayılarının EKOK'unu hesaplayalım.

İlk sayıdaki tabanlar 2, 3 ve 5;
İkinci sayıdaki tabanlar 3, 5 ve 7'dir.

EKOK'ta tüm tabanlar olması gerektiğinden, bu sayı 2^a . 3^b . 5^c . 7^d formundadır.

(a) İlk sayıdaki 2 tabanının kuvveti 1'dir. İkinci sayıda 2 tabanı olmadığı için kuvvetin 0 olduğunu kabul edebiliriz. Bu kuvvetlerden 1 daha büyük olduğu için EKOK'taki 2'nin kuvveti 1 olmalıdır.
(b) İlk sayıdaki 3'ün kuvveti 2 ve ikinci sayıdaki 3'ün kuvveti 4'tür. 4 daha büyük olduğu için EKOK'taki 3'ün kuvveti 4'tür.
(c) İlk sayıdaki 5'in kuvveti 3 ve ikinci sayıdaki 5'in kuvveti 1'dir. 3 daha büyük olduğundan EKOK'taki 5'in kuvvveti 3 olmalıdır.
(d) İlk sayıda 7 tabanı olmadığı için kuvvetinin 0 olduğunu düşünebiliriz. İkinci sayıdaki 7'nin kuvveti ise 3'tür. 3 sayısı 0'dan büyük olduğu için EKOK'taki 7'nin kuvveti 3 olmalıdır.