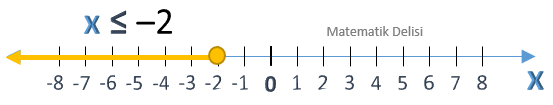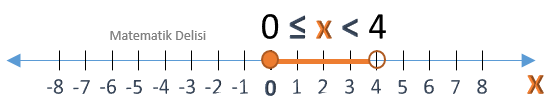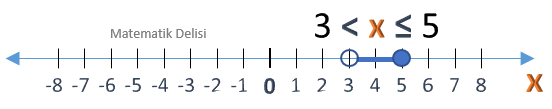BÖLÜM 3: EŞİTSİZLİĞİ SAYI DOĞRUSUNDA GÖSTERME
1. dereceden 1 bilinmeyenli bir eşitsizliğin çözüm kümesi, sayı doğrusunda belli bir aralığa karşılık gelir. Bu aralık,
eşitsizliğin doğru olabilmesi için değişkenin alabileceği değerleri kapsar.
Aşağıdaki örnekleri inceleyelim.
x ≥ 4 eşitsizliğini sayı doğrusunda gösterelim.
Bu eşitsizlik, 4 veya 4’ten büyük tüm x değerleri için doğrudur. 4'ten büyük sayıların çözüm kümesinde olduğunu gösterebilmek için 4'ün sağına bir yarı doğru çizilir. 4'ün eşitsizliği sağladığını belirtmek için de tam bu noktanın üzerine içi dolu küçük bir daire koyulur.
x > –5 eşitsizliğini sayı doğrusunda gösterelim.
Verilen eşitsizlik, –5’ten büyük tüm x değerleri için doğrudur. Bu nedenle –5’in sağında kalan tüm noktalar çözüm kümesindedir. Bu noktalar –5'in sağ tarafına çizilen bir yarı doğru ile gösterilir.
Eşitsizlikte > sembolü kullanıldığı için –5 noktası çözüme dahil değildir. Bu durumu belirtmek için –5'in bulunduğu noktaya içi boş küçük bir daire konur.
x ≤ 3 eşitsizliğini sayı doğrusunda gösterelim.
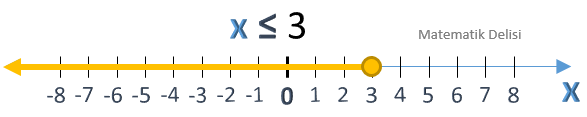
Bu eşitsizlik, 3 veya 3’dan küçük tüm x değerleri için doğrudur. 3'ten küçük sayıların çözüm kümesinde olduğunu gösterebilmek için 3’ün soluna bir yazrı doğru çizilir. x = 3 için de eşitsizlik sağladığından bu noktaya içi dolu küçük bir daire koyulur.
x < 0 eşitsizliğini sayı doğrusunda gösterelim.
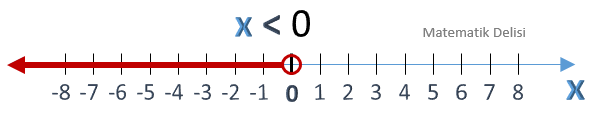
Yukarıdaki eşitsizlik 0’dan küçük tüm x değerleri için doğrudur. Sayı doğrusunda 0'dan küçük gerçek sayılar kümesi, bu noktanın soluna çizilen bir yarı doğru ile gösterilir. x = 0 için eşitsizlik sağlamadığından, 0 noktasına içi boş küçük bir daire çizilir.
BİLEŞİK EŞİTSİZLİKLER
2 ≤ x ≤ 5 eşitsizliğini sayı doğrusunda gösterelim.
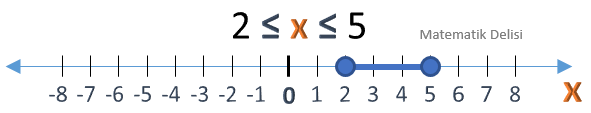
Bu eşitsizlik, 2'den 5'e kadar olan tüm x değerleri için doğrudur. 2 ile 5 arasındaki sayılar, sayı doğrusunda bu noktalar arasına çizilen bir doğru parçası ile gösterilir. Eşitsizlik 2 ve 5 değerleri için de sağladığından her iki noktaya da içi dolu bir daire konur.
–2 < x < 4 eşitsizliğini sayı doğrusunda gösterelim.
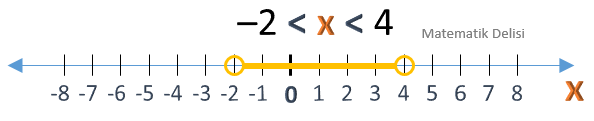
Yukarıdaki eşitsizlik, –2 ile 4 arasındaki x değerleri için doğrudur. Sayı doğrusunda bu aralık –2 ile 4 noktaları arasına çizilen bir doğru parçası ile gösterilir. Sınır noktaları çözüme dâhil olmadığından, bu noktalara içi boş daireler konur.
–5 ≤ x < –2 eşitsizliğini sayı doğrusunda gösterelim.
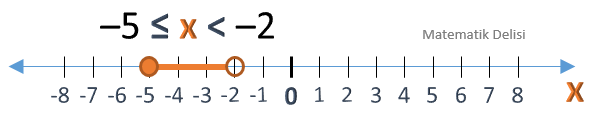
Yukarıdaki eşitsizlik, –5 ile –2 arasındaki tüm x değerleri için doğrudur. –5 sayısı çözüm kümesine dâhil olduğu halde –2 sayısı dâhil değildir. –5 ile –2 arasındaki sayılar, bu noktalar arasına çizilen bir doğru parçası ile gösterilir. –5'in çözüme dâhil olduğunu göstermek için bu noktaya içi dolu bir daire konur. –2'nin dâhil olmadığı ise bu noktaya konulan içi boş bir daire ile gösterilir.
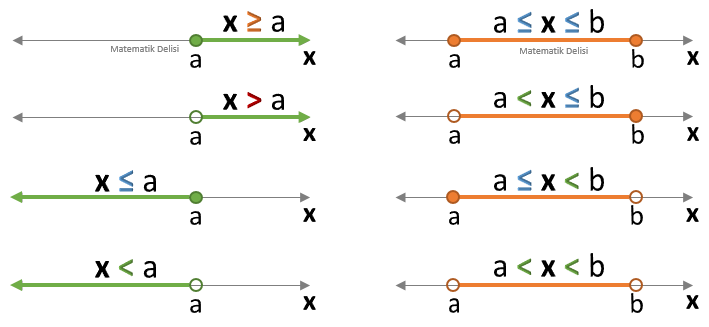
Daha karmaşık eşitsizlikleri sayı doğrusunda göstermeden önce yukarıdaki formlardan birine dönüştürürüz. Bu dönüştürme işlemi aynı zamanda eşitsizliğin çözümüdür.
1. dereceden 1 bilinmeyenli eşitsizliklerin nasıl
çözüldüğünü görmek için sonraki konuyu okuyabilirsiniz.
Aşağıdaki eşitsizlikleri sayı doğrusunda gösterin.
a) x > 0, b) x ≤ –2, c) 0 ≤ x < 4, d) 3 < x ≤ 5
