ÇIKMIŞ SORULAR: EŞOLASILIKLI OLAYLARLA İLGLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-1
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 1 | 2 | 3 | 1 | 1 | 2 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 1 |
| 2018-2019 | 2 |
| 2019-2020 | 3 |
| 2020-2021 | 1 |
| 2021-2022 | 1 |
| 2022-2023 | 2 |
| 2023-2024 | 1 |
Aşağıda, LGS'de olasılıkla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2017-2018 LGS
21 000 m2 lik bir arsa ortaklar arasında paylaştırılacaktır. Paylaşım için arsanın tamamı 250 m2, 500 m2 ve 1000 m2 lik bölümlere ayrılıyor. Toplam bölüm sayısı ortakların sayısına eşittir. Her bir bölüm numaralandırılıyor ve numaralar özdeş kartların üzerine yazılarak boş bir torbaya atılıyor. Arsanın ortakları arasında çekilecek kura ile bu bölümlerin sahipleri belirlenecektir.
Bu kurada torbadan çekilecek ilk kartın üzerinde yazan numaranın; alanı 250 m2, 500 m2 ve 1000 m2 olan bölümlerden birine ait olma olasılıkları eşit olduğuna göre bu arsanın kaç ortağı vardır?
Çözüm:
İlk çekilen numaranın, alanı 250 m2, 500 m2 ve 1000 m2 olan bölümlerden birine ait olma olasılıkları eşitse, bu bölümlerin sayıları eşittir. Alanı aynı olan bölümlerin sayısına x dersek
- Alanı 250 m2 olan bölümlerin toplam alanı 250x;
- Alanı 500 m2 olan bölümlerin toplam alanı 500x; ve
- Alanı 1000 m2 olan bölümlerin toplam alanı 1000x olur.
Buna göre, x cinsinden toplam alan 250x + 500x + 1000x = 1750x'tir. Bu sayı 21 000'e eşit olduğuna göre her çeşit karttan 21 000 ÷ 1750 = 12 tane bulunmaktadır. Dolayısıyla toplam kart sayısı 3 × 12 = 36'dır. Ortak sayısı bölüm sayısına eşit olduğuna göre bu arsanın 36 ortağı vardır.
CEVAP: B
2018-2019 LGS

İçinde kırmızı veya sarı renkli 5 topun bulunduğu 1. torbadan rastgele çekilen bir topun kırmızı olma olasılığı daha fazladır. Ayrıca mavi veya sarı renkli 7 topun bulunduğu 2. torbadan rastgele çekilen bir topun sarı olma olasılığı daha azdır. 1. ve 2. torbadaki topların tamamı boş bir kutuya atılıp karıştırılıyor.
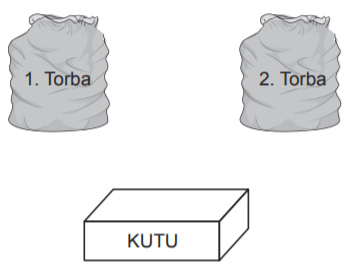
Topların tamamı renkleri dışında özdeş olduğuna göre bu kutudan rastgele çekilen bir topun sarı olma olasılığı en fazla kaçtır?
Çözüm:
1. Torba:
1. torbadan rasgele çekilen bir topun kırmızı gelme olasılığı daha fazlaysa, sarı topların sayısı yarıdan azdır. Buna göre, ilk torbada en fazla 2 sarı top vardır.
2. Torba:
Bu torbadan rasgele çekilen bir topun sarı olma olasılığı daha düşükse, bu torbada da sarı topların sayısı tüm topların yarısından azdır. Buna göre ikinci torbada en fazla 3 sarı top vardır.
Kutu:
Torbalardaki toplar aynı kutuya atıldığında, bu kutuda toplam 5 + 7 = 12 top olur. 12 toptan en fazla 2 + 3 = 5'i sarıdır. Buna göre, kutudan çekilen topun sarı olma olasılığı en fazla ... olabilir.
CEVAP: C
..., ..., ..., ... birer gerçek sayı ve ... ≥ ..., ... ≥ ... olmak üzere
... ...
... dir.

Tablo 1ʼde verilen ifadelerin her biri Tablo 2ʼde verilen ifadelerin her biri ile birer kez çarpılıyor. Bu şekilde elde edilen sayıların her biri, bir karta bir sayı gelecek şekilde özdeş kartlara yazılarak boş bir torbaya atılıyor.
Torbadan rastgele çekilen bir kartın üzerinde yazan sayının doğal sayı olma olasılığının ... olması için A yerine aşağıdakilerden hangisi yazılmalıdır?
Çözüm:
Tablo 1 ve Tablo 2'deki sayıların mümkün olan tüm çarpanlarını kök dışına çıkaralım.

Bu tabloların her birinden birer sayı seçip çarptığımızda, sonucun doğal sayı olabilmesi için her iki sayının da kareköklü kısımlarının aynı olması gerekir. Tablo 1'deki ... ile Tablo 2'deki ... ve ... sayılarının çarpımı doğal sayıdır.
Tabloların her birinden birer sayı seçip çarparak 16 farklı sonuç elde edebiliriz. Bu sonuçlardan rasgele çekilen birinin doğal sayı olma olasılığının ...'e eşit çıkabilmesi için 16 sonuçtan 2'sinin doğal sayı olması gerekir. Yukarıda hâlihazırda 2 çarpımın doğal sayı olduğunu görmüştük. Bu nedenle, A'nın Tablo 2'deki herhangi bir sayı ile çarpımının doğal sayı olmaması gerekir. A sayısı ...'e eşit olduğunda, bu sayıyla yapılan çarpma işlemlerinin sonucu doğal sayı olmaz.
CEVAP: C

Aşağıdaki tabloda • (nokta) ve – (çizgi) karakterleri kullanılarak tanımlanmış rakamlar verilmiştir.
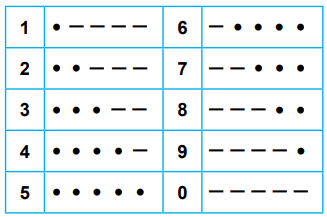
Bu rakamlara karşılık gelen karakterlerle oluşturulan iki basamaklı doğal sayıların tamamı aşağıdaki gibi özdeş kartlara yazılıp boş bir torbaya atılmıştır.
Örneğin,

Bu torbadan rastgele yapılan bir çekilişte üzerindeki • (nokta) sayısı 5 olan kartın çekilme olasılığı kaçtır?
Çözüm:
İki basamaklı 90 doğal sayı vardır. Bu doğal sayıların 17'sinde (50, 14, 41, 16, 61, 94, 49, 96, 69, 27, 72, 38, 83, 87, 78, 23, 32) beş nokta bulunmaktadır. Buna göre istenilen olasılık ...'dır.
CEVAP: C


Kenarlarının uzunlukları 1 m ve 9 m olan dikdörtgen biçimindeki bir halının ön yüzü, şekildeki gibi farklı renklere boyanmıştır. Bu renklerin her birinin kapladığı karesel bölgenin alanı birbirine eşittir.
Bu halı, parçalarda aynı renk olmayacak şekilde iki parçaya bölünecektir.
Buna göre bu parçalardan birinin boyalı yüzünün alanının, diğerinin boyalı yüzünün alanının 2 katı olması olasılığı kaçtır?
Çözüm:
9 renkten oluşan bu halı 8 farklı şekilde bölünebilir. Bu bölünme şekillerinden 2'sinde, parçalardan birinin alanı diğerinin alanının 2 katıdır.
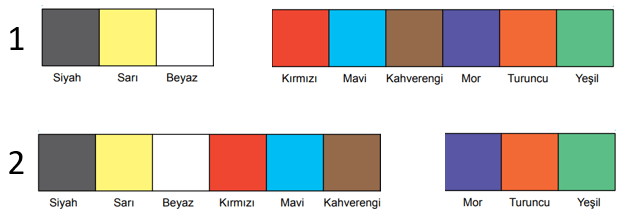
Buna göre istenilen olasılık ...'tür.
CEVAP: B
