ÇIKMIŞ SORULAR: EŞOLASILIKLI OLAYLARLA İLGLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-2
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 1 | 2 | 3 | 1 | 1 | 2 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 1 |
| 2018-2019 | 2 |
| 2019-2020 | 3 |
| 2020-2021 | 1 |
| 2021-2022 | 1 |
| 2022-2023 | 2 |
| 2023-2024 | 1 |
Aşağıda, LGS'de olasılıkla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2020-2021 LGS

Renkleri dışında özdeş olan toplardan 4’ü kırmızı, geri kalanı beyazdır. Bu topların tamamı aşağıdaki boş A, B ve C torbalarına dağıtılıyor.

Bu torbaların her birinden rastgele çekilen bir topun kırmızı olma olasılığı birbirine eşittir.
Buna göre başlangıçtaki beyaz top sayısı aşağıdakilerden hangisi olamaz?
Çözüm:
Torbalardan birine hiç kırmızı top atılmamış olsaydı, bu torbadan çekilen topun kırmızı olma olasılığı 0 olurdu. Yalnız bu durumda, torbalardan rasgele çekilen topların kırmızı olma olasılıkları birbirine eşit olamazdı. Bu nedenle her torbaya en az 1 kırmızı top atılmıştır.
4 kırmızı top 3 torbaya her birinde en az 1 kırmızı top olacak şekilde dağıtıldığında, torbalardan ikisine birer tane ve birine iki tane kırmızı top düşer. Kırmızı top çekme olasılıklarınıın eşit olabilmesi için 1 kırmızı top atılan torbalarda eşit sayıda ve 2 kırmızı top atılan torbaya diğerlerinin 2 katı kadar beyaz top eklenmesi gerekir.
İçinde 1 kırmızı top olan torbalardaki beyaz top sayısına x dersek içinde 2 kırmızı top olan torbadaki beyaz top sayısı 2x olur. Buna göre beyaz topların toplam sayısı x + x + 2x = 4x şeklinde ifade edilebilir. x bir doğal sayı olduğundan 4x sayısı 4'e kalansız bölünür. Seçeneklerdeki 82 sayısı 4'e kalansız bölünmediği için beyaz topların toplam sayısı 82 olamaz.
CEVAP: B
... ve ..., ... tam sayılar olmak üzere
... ve ... dir.

Aşağıda kenarlarının uzunlukları 25 mm ve 84 mm olan dikdörtgen şeklinde bir karton verilmiştir.

Bu karton, kenarlarının uzunluğu 25 mm olan kare şeklindeki eş parçalara aşağıdaki gibi ayrılarak sırasıyla sarı, kırmızı, mavi, yeşil ve turuncu renklere boyanıyor. Her bir kare şekildeki gibi kesilerek boş bir torbaya atılıyor.

Bu torbadan rasgele çekilen bir karenin kırmızı kare olma olasılığı kaçtır?
Çözüm:
Kare şeklindeki parçalardan her birinin genişliği 25 mm'dir. Kesilen parça sayısını bulabilmek için kartonun genişliğini parçalardan birinin genişliğine bölebiliriz.
... ... ... ...
Bu parçalar, beşerli gruplar halinde soruda belirtilen renklere boyanmıştır. İlk 125 parçada her renkten 125 ÷ 5 = 25 kare vardır. Son 3 parçadan ilki sarı, ikincisi kırmızı ve üçüncüsü mavidir. Buna göre, toplam 26 sarı, 26 kırmızı, 26 mavi, 25 yeşil ve 25 turuncu parça vardır. Rasgele seçilen bir parçanın kırmızı olma olasılığı, kırmızı parça sayısının tüm parçaların sayısına oranlanmasıyla bulunabilir.
...
CEVAP: C
2021-2022 LGS
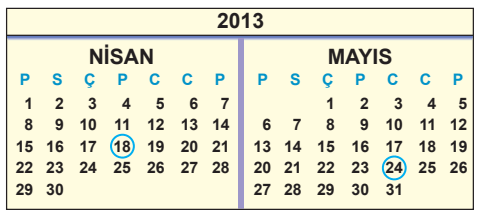
Öğrenci sayısı 20 olan bir sınıftaki her bir öğrencinin doğum tarihi birbirinden farklıdır. Bu sınıfın öğrenci listesi, öğrencilerin doğum tarihlerine göre büyükten küçüğe doğru sıralanarak oluşturulmuştur. Listenin ilk sırasındaki öğrencinin doğum tarihi 18 Nisan 2013, son sırasındaki öğrencinin doğrum tarihi 24 Mayıs 2013 olmuştur.
Bu listeden rasgele seçilen bir öğrencinin doğum tarihinin nisan ayında olma olasılığı, mayıs ayında olma olasılığından daha fazladır.
Buna göre, doğum tarihi 25 Nisan 2013'ten önce olan en az kaç öğrenci vardır?
Çözüm:
Rasgele seçilen bir öğrencinin doğum tarihinin nisan ayında olma olasılığı mayıs ayında olma olasılığından fazlaysa 20 öğrenciden en az 11'i nisan ayında doğmuştur. 18 Nisan'da doğan öğrenciyi çıkardığımızda geriye 10 öğrenci kalır. Nisan ayında, ayın 25'i ve sonrasında toplam 6 gün bulunmaktadır. Geriye kalan 10 öğrenciden en fazla 6'sının doğum günü bu günlere denk gelebilir. Buna göre, nisan ayının 18'i ile 25'i arasında en fazla 4 öğrencinin doğum günü olabilir. Ayın 18'inde doğan öğrenciyi de ekleyerek cevabın 5 olduğunu görebiliriz.
CEVAP: C
2022-2023 LGS
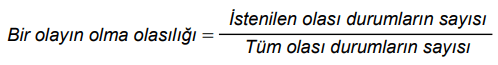
Aşağıda verilen abaküste üç basamaklı 423 sayısı modellenmiştir.
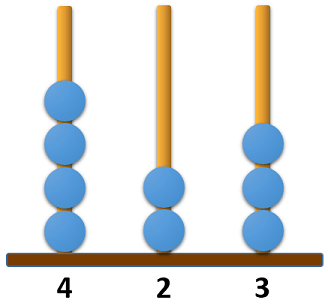
Bu abaküsteki boncuklardan bir tanesi, bulunduğu çubuktan çıkarılarak diğer çubuklardan birine takılıyor.
Buna göre, abaküste modellenen yeni sayının 500'den büyük olma olasılığı kaçtır?
Çözüm:
6 farklı durumla karşılaşabiliriz.
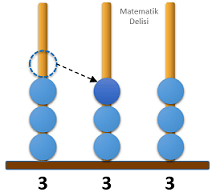
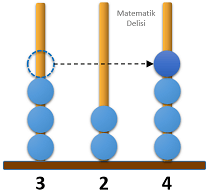
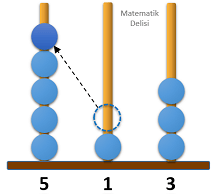
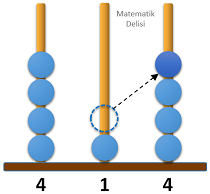
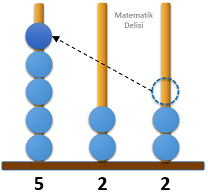
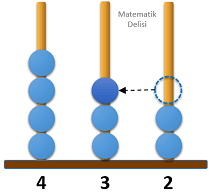
6 durumun 2'sinde 500'den büyük bir sayı elde ettiğimiz için yeni sayının 500'den büyük olma olasılığı ...'tür.
CEVAP: B
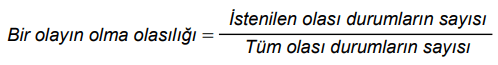
Renkleri dışında özdeş olan yeterli sayıda top vardır. Bu toplar, her bir kutuda eşit sayıda top olacak şekilde başlangıçta boş olan I, II, III ve IV numaralı kutulara yerleştiriliyor.
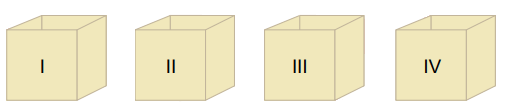
Kutulardaki toplar, boş olan A, B, C torbalarında tablodaki gibi birleştirilirse bu torbalardan rasgele çekilen birer topun mavi olma olasılıkları tablodaki gibi olmaktadır.

Buna göre, başlangıçtaki bu dört kutuda bulunan mavi top sayısı aşağıdakilerden hangisi olabilir.
Çözüm:
I. ve II. kutular birleştirildiğinde rasgele çekilen bir topun mavi çıkma olasılığı %100 ise hem I. hem de II. kutudaki topların tümü mavidir.
Verilen tabloya göre, I ve III. kutuların birleşiminden çekilen rasgele bir topun mavi olma olasılığı ise %75'tir. Olasılığın %75 = ... olması, bu iki kutunun birleşiminde her 4 toptan 3'ünün mavi olduğunu gösterir. Bu topların yarısı I. ve diğer yarısı III. kutudadır. Her 4 toptan 2'si I. kutudan gelen mavi toplar olduğundan, geriye kalan 2 toptan yalnız 1'i mavidir. Bu toplar III. kutudan geldiğine göre, bu kutudaki her 2 toptan 1'i mavidir.
I. ve IV. kutuların birleşiminden çekilen rasgele bir topun mavi olma olasılığı %50'dir. Olasılığın %50 olması bu birleşimdeki topların yarısının mavi olduğunu gösterir. Bu topların yarısının I. kutudan geldiği ve I. kutudaki tüm topların mavi olduğu göz önünde bulundurulduğunda IV. kutuda hiç mavi top olmadığı sonucu çıkarılabilir.
Özetle,
- I. kutudaki tüm toplar mavidir.
- II. kutudaki tüm toplar mavidir.
- III. kutudaki topların yarısı mavidir.
- IV. kutuda hiç mavi top yoktur.
- Tüm kutularda eşit sayıda top vardır.
III. kutudaki mavi top sayısına 1 birim dersek, I. ve II. kutularda 2'şer birim mavi top vardır. Buna göre, kutulardaki toplam mavi top sayısı 2 + 2 + 1 = 5 birimdir. Mavi top sayısının 5 birim olması, bu sayının 5'in tam katlarından biri olduğu anlamına gelir. Sadece A seçeneğindeki 15 sayısı, 5'in tam katıdır.
CEVAP: A
