ÇIKMIŞ SORULAR: KAREKÖK VE TAM SAYILARLA İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-2
Aşağıda, TEOG sınavlarında karekök ve tam sayılarla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki sayfaya geçebilirsiniz.
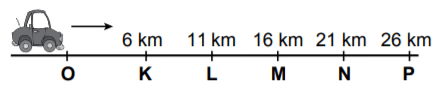
Şekilde O noktasında bulunan bir aracın K, L, M, N, P noktalarına uzaklıkları verilmiştir.
Bu araç ok yönünde ... km yol aldığında bulunduğu yer, hangi ardışık iki nokta arasında olur?
Çözüm:
210'dan büyük ve 210'a en yakın tam kare sayı 152 = 225'tir. Bu nedenle, ... sayısı 14 ile 15 arasındadır. 14 ile 15 arasındaki bir nokta, aynı zamanda L ile M noktaları arasındadır.
CEVAP: D
2016-2017 TEOG

Şekildeki sayı doğrusunda L noktasına karşılık gelen sayı 9'dur.
K ile L noktaları arasındaki uzaklık ... birim olduğuna göre K noktasına karşılık gelen sayı aşağıdaki hangi iki sayı arasındadır?
Çözüm:
Sayı doğrusunda 9'un ... birim solundaki nokta ...'dir.
27'den küçük ve 27'ye en yakın tam kare sayı 52'dir. Bu nedenle ... sayısı 5 ile 6 arasındadır.
... ifadesinde ... yerine sırasıyla 6 ve 5 sayılarını koyarak, bu ifadenin 3 ile 4 arasında olduğunu görebiliriz.
CEVAP: B
Aşağıdakilerden hangisi sayı doğrusunda 8 ile 9 arasında ve 9'a daha yakındır?
Çözüm:
8 ile 9 arasındaki kareköklü ifadelerde, karekök içerisindeki sayı 82 = 64 ile 92 = 81 arasındadır. A, B ve C seçeneğindeki sayılar bu özelliğe uymaktadır.
Böyle bir ifadenin 9'a daha yakın olabilmesi için karekök içerisindeki sayının 81'e 64'ten daha yakın olması gerekir. 65 ve 72 sayıları 64'e daha yakındır. 80 ise 81'e daha yakındır. Bu nedenle cevap C'dir.
CEVAP: C
