ÇIKMIŞ SORULAR: KAREKÖK VE TAM SAYILARLA İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-2
Aşağıda, LGS sınavlarında karekök ve tam sayılarla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki sayfaya geçebilirsiniz.
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 2 | 0 | 2 | 1 | 1 | 1 | 2 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 2 |
| 2018-2019 | 0 |
| 2019-2020 | 2 |
| 2020-2021 | 1 |
| 2021-2022 | 1 |
| 2022-2023 | 1 |
| 2023-2024 | 2 |
2021-2022 LGS
Kare şeklindeki sarı, mavi ve beyaz kartlar, ikişer kenarları ve birer köşeleri A noktasında çakışacak biçimde üst üste yapıştırılarak aşağıdaki şekil elde edilmiştir.
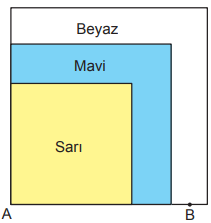
Şekilde görünen farklı renkteki bölgelerin alanları birbirine eşit ve sarı bölgenin çevresinin uzunluğu 20 cm'dir.
A noktasına uzaklığı santimetre cinsinden doğal sayı olacak biçimde, beyaz bölgenin kenarında şekildeki gibi bir B noktası işaretleniyor.
Buna göre, A ve B noktaları arasındaki uzaklık kaç santimetredir?
Çözüm:
Çevresi 20 cm olan kare şeklindeki sarı bölgenin kenar uzunluğu 20 ÷ 4 = 5 cm ve alanı 5 × 5 = 25 cm2'dir.
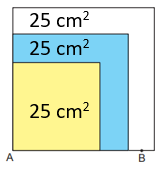
Farklı renkteki alanlar birbirine eşit olduğu için mavi kartın toplam alanı 25 + 25 = 50 cm2 ve beyaz kartın toplam alanı 50 + 25 = 75 cm2'dir.
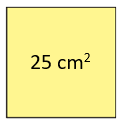
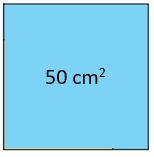
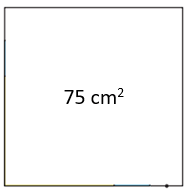
- Mavi kartın kenar uzunluğu ... cm ve
- Beyaz kartın kenar uzunluğu ... cm'dir.
Buna göre A ve B noktaları arasındaki uzaklık ... cm ile ... cm arasındadır.
50 ile 75 arasındaki tek tam kare sayı 64 olduğundan A ile B arasındaki mesafe ... = 8 cm olabilir.
CEVAP: B
2022-2023 LGS
..., ... birer doğal sayı olmak üzere
... dir.
Yükseklikleri 5 m ve 6 m olan A ve B direkleri arasına, boyu 2 m olan bir fidan dikilmiştir.
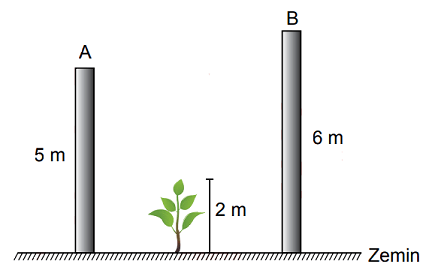
Bir süre sonra bu fidanın boyu A direğinin yüksekliğinden fazla, B direğinin yüksekliğinden az olmuştur.
Buna göre bu fidan, dikildikten sonra kaç metre uzamış olabilir?
Çözüm:
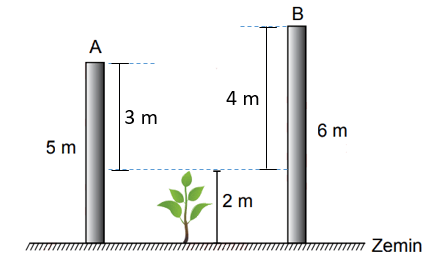
Bu fidanın boyu 3 m ile 4 m arasında uzamıştır. Seçeneklerde verilen kareköklü ifadelerin hangi tam sayılar arasında olduklarını bulalım.
8'e en yakın tam kare sayılar 22 = 4 ve 32 = 9'dur. Buna göre,
... sayısı
12'ye en yakın tam kare sayılar 32 = 9 ve 42 = 16'dır. Dolayısıyla,
... ifadesinin değeri
18'e en yakın tam kare sayılar 42 = 16 ve 52 = 25'tir. Bu nedenle,
... ifadesi
24'e en yakın tam kare sayılar 42 = 16 ve 52 = 25'tir. Bu ifade de
CEVAP: B
2023-2024 LGS
Bir televizyonun ses seviyesi ile ses göstergesi arasındaki ilişki aşağıda verilmiştir. Bu ilişkide, ses seviyesini gösteren sayı tam kare ise karekök değeri, tam kare değil ise karekök değerinin en yakın olduğu doğal sayı değeri, hoparlör sembolünün yanındaki çizgi sayısı ile gösterilmiştir.
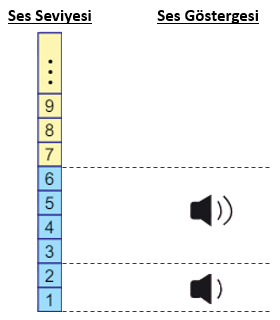
Bu televizyonun ses göstergesi  iken,
ses seviyesi en fazla kaçtır?
iken,
ses seviyesi en fazla kaçtır?
Çözüm:
Hoparlörün yanındaki çizgi sayısı ses seviyesinin kareköküne en yakın tam sayıyı göstermektedir. Sorudaki göstergede 3 çizgi bulunmaktadır. Biz de kareköküne en yakın tam sayı 3 olan sayılardan en büyüğünü bulacağız. 9 ile 16 arasındaki sayılardan 9'a daha yakın olanların karekökü 3'e ve 16'ya daha yakın olan en büyük sayı 12'dir.
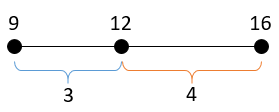
Buna göre, ses seviyesi en fazla 12 olabilir.
CEVAP: C
Aşağıda uzunluğu 7 birim, genişliği 2 birim olan dikdörtgen şeklinde bir yol modellenmiştir. [EA]'nın uzunluğu 3 birimdir. Bu modele göre A noktasına 1 adet tabela yerleştirilmiştir. [BC] üzerindeki bir noktaya da 1 adet tabela yerleştirilecektir. Bu noktanın A noktasına uzaklığı birim cinsinden doğal sayı olacaktır.
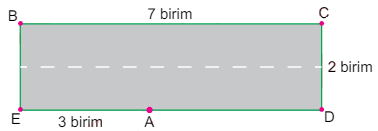
Buna göre, bu tabela B ile C arasındaki kaç farklı noktaya yerleştirilebilir?
Çözüm:
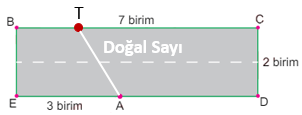
BC doğru parçası üzerine yerleştirilen ikinci tabelayı T ile göstermek |AT| uzunluğu bir doğal sayı olmalıdır.
T noktası A'nın tam karşısında, solunda veya sağında olabilir.
A'nın Tam Karşısı:
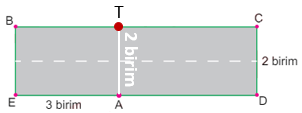
T noktası A'nın tam karşısında ise aralarındaki uzaklık 2 birim olur ve bu bir doğal sayıdır.
A'nın Solu:
T noktasından ED doğru parçasına bir dik indirirsek, köşe noktalarından ikisi A ve T olan bir dik üçgen elde ederiz. Bu dik üçgenin hipotenüsü AT doğru parçasıdır.
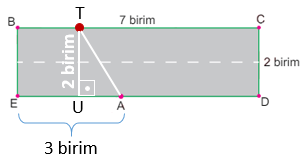
AUT üçgeninde |UA| uzunluğu en fazla 3 olabilir. Buna göre, |AT| uzunluğunun karesi en fazla 22 + 32 = 13 olabilir. Karesi 13'ten küçük doğal sayılar 0, 1, 2 ve 3'tür. Bir dik üçgendeki en uzun kenar hipotenüstür. Dolayısıyla, |AT| uzunluğu 2'den büyüktür. Bulduğumuz sayılar içinde 2'den büyük olan tek sayı 3'tür.
A'nın Sağı:
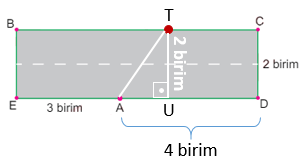
T noktası A'nın sağında olduğu durumda |AU| uzunluğu en fazla 4 olabilir. Buna göre |AT| uzunluğunun karesi en fazla 22 + 42 = 20'dir. Karesi 20'den küçük olan doğal sayılar 0, 1, 2, 3 ve 4'tür. Hipotenüs uzunluğu 2'den büyük olması gerektiği için |AT|'nin alabileceği değerler 3 ve 4'tür.
Nokta Sayısı:
Biri A'nın tam karşısında, biri A'nın solunda ve ikisi A'nın sağında olmak üzere soruda verilen şartlara uyan toplam 4 nokta belirlenebilir.
CEVAP: C
