BÖLÜM 2: OLASILIKTA DENEY, ÇIKTI VE OLAY
DENEY
Olasılık içeren tüm eylemler ve durumlar, olasılık deneyleridir.
- Zar atmak,
- Yazı-tura atmak,
- Öğrenciler arasından sınıf başkanı seçmek ve
- Kutulardan renkli toplar çekmek,
birer deneydir.
Olasılıktaki deneyin, gerçek bir deney olması şart değildir.
ÇIKTI
Bir deneyin olası sonuçlarından her birine çıktı adı verilir.
- Yazı-tura atma deneyinin iki farklı çıktısı vardır:
Yazı veTura - Zar atma deneyinin 6 farklı çıktısı vardır:
1 ,2 ,3 ,4 ,5 ve6 . - Sınıf başkanı seçme deneyinin çıktıları başkanlığa aday olan öğrencilerdir.
- İçerisinde 10 adet renkli top bulunan bir kutudan rasgele bir top çekme deneyinin çıktıları kutu içerisindeki toplardır.
Bir olasılık deneyinin tüm çıktıları, bir küme oluşturur. Yazı-tura ve zar atma deneylerinin çıktıları yukarıda
gösterilmiştir.
OLAY
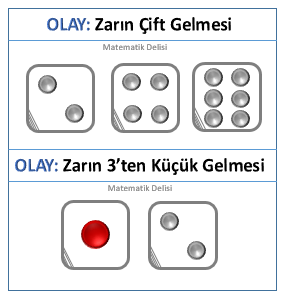
Olay, olasılığı merak edilen çıktılar bütünüdür. Olasılığı bulunabilen her şey,
olay olarak tanımlanabilir.
- Zar atma deneyinde, "zarın çift gelmesi" bir olaydır. Aynı deneyde "zarın 3’ten küçük gelmesi" farklı bir olaydır. "Zarın 5 gelmesi" ise diğer bir olaydır. Bu olayların tümünün olasılığı bulunabilir.
- Yazı-tura atma deneyinde, "sonucun yazı gelmesi" bir olaydır, "tura gelmesi" ise farklı bir olaydır.
- Sınıf başkanı seçme deneyinde "Ahmet’in sınıf başkanı olması", "sınıf başkanının kız olması", "sınıf başkanının kilosunun 50 kg’dan fazla olması" birer olaydır.
- Kutudan top çekme deneyinde, "çekilen topun renginin kırmızı olması" bir olaydır.
Olay, aynı zamanda çıktılar kümesinin alt kümesi olarak da tanımlanabilir. Olayların kümeler ve
olasılıkla ilişkisini bir sonraki bölümde inceliyoruz.
Bazı kaynaklarda, olasılığın bir “olay”, bazılarında ise bir “sonuç” olarak tanımlandığını görüyoruz. Olasılık ne olay ne de sonuçtur; ağırlık gibi, uzunluk gibi bir ölçüdür. İleri düzey matematikte, Ölçü Teorisi (İng. Measure Theory) adı verilen bir alan vardır. Bu alan içerisindeki ölçü tanımına uyduğu için olasılık, matematikte belirsizliğin bir ölçüsü ( İng. a measure of uncertainty) olarak tanımlanır.
