BÖLÜM 3: OLASILIK VE KÜMELER

Çıktı, olay ve olasılık kavramları kümeler konusuyla yakından ilişkilidir. Olasılıkla ilgili kavramların daha iyi anlaşılabilmesi için çıktıları, olayları ve bu olayların olasılıklarını kümeleri kullanarak tekrar inceliyoruz.

ÇIKTILAR VE KÜMELER

Bir olasılık deneyinin tüm çıktıları bir küme oluşturur. Bu kümeye çıktılar kümesi ismi verilir. Örneğin, yazı-tura atma deneyinin çıktılar kümesi solda ve zar atma deneylerinin çıktılar kümesini sağdaki gibidir.

OLAYLAR VE KÜMELER

Çıktılar kümesinin elemanlarıyla oluşturulan alt kümelerden her biri birer olaydır. Yukarıda zar atma deneyine ait iki farklı olay ve bu olaylara ilişkin alt kümeleri görüyoruz.

İMKANSIZ OLAYLAR

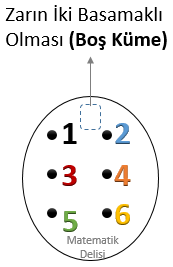
Bir olay, çıktıların hiçbiri ile bağdaşmıyorsa, boş küme ile gösterilebilir. Örneğin, zar atma deneyinde iki basamaklı bir çıktı olmadığı için "atılan zarın iki basamaklı bir sayı gelmesi" olayı boş kümeye denktir.

Çıktılar kümesinde boş küme ile gösterilen olaylar, imkânsız olaylardır ve bu olayların olasılıkları 0'dır.

KESİN OLAYLAR

Bir olay, çıktıların tamamını kapsıyorsa, bu olayın kümesi çıktılar kümesine eşittir. Örneğin, zar atma deneyinde tüm çıktılar tek basamaklı olduğu için "atılan bir zarın tek basamaklı olması" olayı çıktılar kümesi ile aynıdır.

Çıktılar kümesinin tümünü kapsayan olaylar, kesin olaylardır ve bu olayların olasılıkları 1'e eşittir.

OLAYLAR VE OLASILIK

BİR ÇIKTININ OLASILIĞI

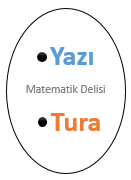
Çıktılar kümesindeki elemanlardan her birinin 0 ile 1 arasında bir olasılık değeri vardır. Örneğin, bir yazı-tura atma deneyinde hilesiz bir para kullanılmışsa, hem yazı hem de tura gelme olasılıkları 0,5'tir. Hileli bir para için ise, yazı gelme olasılığı 0,8 iken, tura gelme olasılığı 0,2 olabilir.

OLASILIKLARIN TOPLAMI

Çıktılar kümesindeki elemanların olasılık değerlerinin toplamı 1'dir. Örneğin, hem hilesiz hem de hileli para atma deneylerinde yazı ve tura gelme olasılıklarının toplamı 1'e eşittir.

Hilesiz para: 0,5 + 0,5 = 1
Hileli para: 0,8 + 0,2 = 1

BİR OLAYIN OLASILIĞI

Bir olayın olasılığını hesaplayabilmek için,

çıktılar kümesindeki hangi elemanların bu olayı tanımlayan altkümede olduğunu bulur,
bulduğumuz elemanların olasılıkları toplarız.

ÖRNEK:

1 gelme olasılığı: 0,2
2 gelme olasılığı: 0,1
3 gelme olasılığı: 0,2
4 gelme olasılığı: 0,3
5 gelme olasılığı: 0,1
6 gelme olasılığı: 0,1

olan bir zarın 4 veya daha büyük gelme olasılığını bulalım.

Bu deneyin 6 çıktısı vardır. Çıktılar kümesi aşağıdaki gibidir.

{1, 2, 3, 4, 5, 6}

Soruda bahsedilen olay, çıktılar kümesinin bir alt kümesidir. Zarın 4 veya daha büyük bir sayı gelmesi, çıktılar kümesindeki 4, 5 ve 6 elemanlarından oluşur. Bu çıktıların olasılıkları sırasıyla 0,3, 0,1 ve 0,1'dir. Bu sayıları toplayarak, zarın 4 veya daha büyük bir sayı gelme olasılığının 0,5 olduğunu görebiliriz.

0,3 + 0,1 + 0,1 = 0,5

NOT: Tüm çıktılara ait olasılıkları topladığımızda, sonucun 1'e eşit olduğuna dikkat edelim.

0,2 + 0,1 + 0,2 + 0,3 + 0,1 + 0,1 = 1

Sonraki konuda, tüm çıktıların aynı olasılığa sahip olduğu durumları inceliyoruz.