ÇIKMIŞ SORULAR: TAM KARE SAYILAR VE KAREKÖKLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ

Tam kare sayılar ve karekökleri ile ilgili LGS'de (Liselere Giriş Sınavında) çıkan soruları ve bu soruların çözümlerini aşağıda bulabilirsiniz.

LGS'DE ÇIKAN SORU SAYISI
	2017-2018	2018-2019	2019-2020	2020-2021	2021-2022	2022-2023	2023-2024
Soru Sayısı	1	1	1	2	0	0	0

LGS'DE ÇIKAN SORU SAYISI
	Soru Sayısı
2017-2018	1
2018-2019	1
2019-2020	1
2020-2021	2
2021-2022	0
2022-2023	0
2023-2024	0

(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)

2017-2018 LGS

Soru 1: (2017-2018 LGS Sınav Sorusu)

Altan ve Can, defterlerine kenar uzunlukları santimetre cinsinden doğal sayı olan birer kare çiziyorlar. Altan'ın çizdiği karenin alanı kenar uzunlukları 7 cm ve 9 cm olan bir dikdörtgenin alanından büyük, Can'ın çizdiği karenin alanı ise bu dikdörtgenin alanından küçüktür.

Buna göre Altan ve Can'ın çizdiği karelerin alanları arasındaki fark en az kaç santimetrekaredir?

A) 8

B) 15

C) 32

D) 39

Çözüm:

Altan ve Can'ın çizdiği karelerin kenar uzunlukları doğal sayı olduğu için alanları tam karedir.

Soruda verilen dikdörtgenin alanı 7 × 9 = 63 cm²'dir. Bu bilgilere göre,

Altan'ın çizdiği karenin alanı, 63'ten büyük bir tam karedir. (Örneğin, 64, 81, 100 vb.)
Can'ın çizdiği karenin alanı, 63'ten küçük bir tam karedir. (Örneğin, 49, 36, 25 vb.).

Altan'ın çizdiği karenin alanı en az 64 cm²'dir. Can'ın çizdiği karenin alanı ise en fazla 49 cm²'dir. Buna göre, karelerin alanları arasındaki fark en az 64 – 49 = 15 cm² olabilir.

CEVAP: B

2018-2019 LGS

Soru 2: (2018-2019 LGS Sorusu)

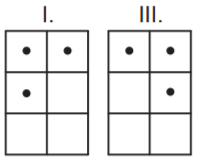
Braille alfabesi görme engellilerin okuyup yazmaları için geliştirilmiş bir yazı sistemidir. Braille rakamları da aşağıdaki gibi tanımlanmıştır.

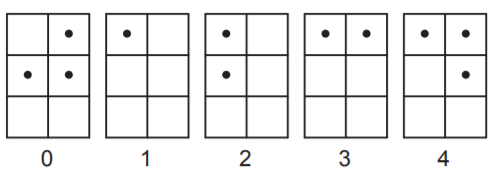
Bu rakamlar kullanılarak aşağıdaki gibi dört haneli bir şifre oluşturulacaktır.

Bu dikdörtgenlerden I. ile II. ve III. ile IV. dikdörtgen aşağıdaki gibi uzun kenarları boyunca çakıştırıldıklarında bu dikdörtgenlerin belirttiği Braille rakamları çakışma kenarlarına göre birbirinin yansıması olacaktır.

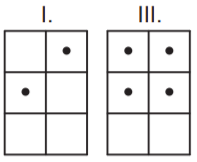
Yukarıdaki gibi oluşturulacak bu şifrede I. ve II. dikdörtgenlerdeki Braille rakamlarından oluşan iki basamaklı sayı tam kare, III. ve IV. dikdörtgenlerdeki Braille rakamlarından oluşan iki basamaklı sayı asal sayı olacaktır.

Buna göre I. ve III. haneye gelmesi gereken Braille rakamları aşağıdakilerden hangisidir?

Çözüm:

Çakışan kenarlara göre birbirinin yansıması olan rakamlar aşağıdaki gibidir.

0 ⟷ 8
3 ⟷ 3
4 ⟷ 6
5 ⟷ 9
7 ⟷ 7

Soruda verilen alfabeye göre seçeneklerdeki sayılar aşağıdaki gibidir.

A) I: 9, III: 7
B) I: 6, III: 5
C) I: 6, III: 4
D) I: 4, III: 8

A Seçeneği:

9 ile 5 birbirinin yansıması olduğundan, ilk sayı 95'tir. Yalnız, 95 tam kare olmadığı için doğru cevap A olamaz.

B Seçeneği:

6 ile 4 birbirinin yansımasıdır. Buna göre ilk sayı 64'tür. 64 tam karedir.

5 ile 9 birbirinin yansımasıdır. 59 asal olduğu için doğru cevap B'dir.

C seçeneği:

C seçeneğinde elde edilen iki basamaklı sayılar 64 ve 46'dır. 64 tam kare olduğu halde 46 asal değildir. Doğru cevap C seçeneği olamaz.

D seçeneği:

D seçeneğinde elde edilen iki basamaklı sayılar ise 46 ve 80'dir. 46 tam kare ve 80 asal değildir. Doğru cevap D seçeneği de olamaz.

CEVAP: B

2019-2020 LGS

Soru 3: (2019-2020 LGS Sorusu)

Dikdörtgen şeklindeki bir kâğıt, alanları santimetrekare cinsinden 10’dan büyük birer tam kare pozitif tam sayıya eşit olan karesel bölgelere aşağıdaki gibi ayrılmıştır.

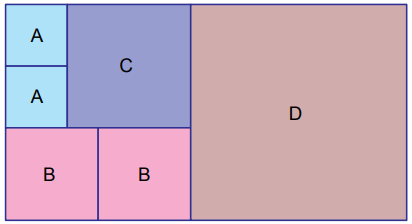
Eşit alanlı bölgeler aynı harf ile gösterildiğine göre dikdörtgen şeklindeki bu kâğıdın bir yüzünün alanı en az kaç santimetrekaredir?

A) 168

B) 255

C) 364

D) 392

Çözüm:

10'dan büyük tam kare sayıların en küçüğü 16 olduğu için en küçük kare olan A'nın alanı en az 16 cm²'dir. Bu durumda, A'nın kenar uzunluğu ... cm ve C'nin kenar uzunluğu 4 + 4 = 8 cm olur.

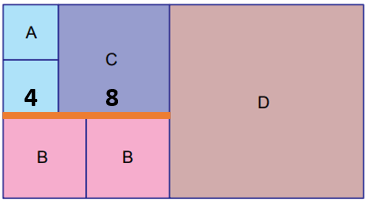
A ve C'nin kenar uzunluklarının toplamı B'nin kenar uzunluğunun 2 katına eşittir. Dolayısıyla, B'nin kenar uzunluğu (4 + 8) ÷ 2 = 6 cm'dir.

D'nin kenar uzunluğu 8 + 6 = 14 cm'dir.

Yukarıda bulduğumuz kenar uzunluklarına göre toplam alan 364 cm²'dir.

4² + 4² + 8² + 6² + 6² + 14² = 364 cm²

CEVAP: C

2020-2021 LGS

Soru 4: (2019-2020 LGS Sorusu)

Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi kısa kenarlarına paralel olarak kesildiğinde dikdörtgen şeklinde iki parça elde edilmiştir.

Elde edilen bu parçalar kısa kenarlarına paralel olarak tekrar kesildiğinde aşağıdaki gibi birbirine eş ikişer kare oluşmuştur. Bu karelerden her birinin bir kenar uzunluğu santimetre cinsinden birer doğal sayıdır.

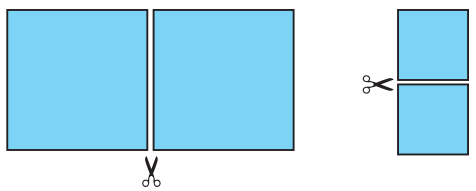
Buna göre başlangıçtaki kâğıdın bir yüzünün alanı santimetrekare cinsinden aşağıdakilerden hangisi olamaz?

A) 40

B) 90

C) 160

D) 240

Çözüm:

Oluşturulan küçük karelerin kenar uzunluklarına x cm dersek , büyük karelerin kenar uzunlukları 2x cm olur. Dolayısıyla, santimetrekare cinsinden

her bir küçük karenin alanı x . x = x² ve
her bir büyük karenin alanı 2x . 2x = 4x²

şeklinde ifade edilebilir. Buna göre, başlangıçtaki kâğıdın bir yüzü

x² + x² + 4x² + 4x² = 10x² cm²

çıkar. x bir doğal sayı olduğundan x² bir tam karedir. 10x² ifadesi ise bir tam karenin 10 katıdır. Bir tam karenin 10 katı olmayan tek seçenek 240'tır. 240 sayısı, santimetrekare cinsinden başlangıçtaki kâğıdın bir yüzünün alanı olamaz.

CEVAP: D

Soru 5: (2019-2020 LGS Sorusu)

... ve ..., ... tam sayılar olmak üzere

... ve ...

Aşağıda, her bir hücresinde 2'nin birbirinden farklı tam sayı kuvvetlerinin yazılı olduğu iki sütunlu bir tablo verilmiştir. Tabloda bu üslü ifadelerden ikisi E ve F harfleriyle gösterilmiştir.

I. Sütun	II. Sütun
2^–1	2^–2
E	F
2³	2¹

I.sütundaki üç üslü ifadenin çarpımı tam kare pozitif bir tam sayıya ve II. sütundaki üç üslü ifadenin çarpımı da tam kare pozitif bir tam sayıya eşittir.

Buna göre E + F en az kaçtır?

A) 33

B) 17

C) 9

D) 3

Çözüm:

Tablodaki E ve F sayılarını sırasıyla 2^e ve 2^f şeklinde gösterdiğimizde

1. sütundaki sayıların çarpımı

2^–1 . 2^e . 2³ = 2^{–1 + e + 3} = 2^{e + 2}'ye ve
2. sütundaki sayıların çarpımı

2^–2 . 2^f . 2¹ = 2^{–2 + f + 1} = 2^{–1 + f}'ye eşit çıkar.

Bu ifadelerin tam kare olabilmesi için kuvvetlerinin 0 veya pozitif çift sayı olması gerekir. Buna göre e + 2 ve –1 + f sayıları ya 0 ya da pozitif çift sayıdır. Bu şartı sağlayan

e değerleri : –2, 0, 2, 4, 6,... ve
f değerleri : 1, 3, 5, 7, 9,...'dur.

Tablodaki sayıların birbirinden farklı olması gerektiği için e kuvveti –2 değerini ve f kuvveti 1 veya 3 değerini alamaz. Buna göre, e'nin alabileceği en küçük değer 0 ve f'nin alabileceği en küçük değer 5'tir. e = 0 ve f = 5 için E + F toplamı 33'e eşittir.

E + F = 2⁰ + 2⁵ = 1 + 32 = 33

CEVAP: A

→KONU ANASAYFASINA DÖN←