ÇIKMIŞ SORULAR: ÜÇGENİN KENAR UZUNLUKLARI VE AÇILARI İLE İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-2

Aşağıda, TEOG sınavlarında üçgenin kenar ve açılarıyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki veya sonraki sayfaya geçebilirsiniz.

Soru 6: (2014-2015 TEOG 2. Dönem Mazeret Sınavı Sorusu)

Bir çeşitkenar üçgenin kenarlarından ikisinin uzunlukları 6 cm ve 7 cm’dir.

Bu üçgenin üçüncü kenarının uzunluğunun santimetre cinsinden alabileceği kaç tam sayı değeri vardır?

A) 7

B) 8

C) 9

D) 10

Çözüm:

Üçgenin bir kenar uzunluğu, diğer iki kenar uzunluğunun toplamı ile farkı arasındadır. Kenarlardan ikisi 6 cm ve 7 cm uzunluğunda olduğuna göre üçüncü kenarın uzunluğu 6 + 7 = 13 cm'den küçük ve 7 – 6 = 1 cm'den büyüktür. 13'ten küçük ve 1'den büyük tam sayılar

2, 3, 4, 5, 6, 7, 8, 9, 10, 11 ve 12'dir.

Yalnız, üçgenin çeşitkenar olduğu için bu listeden 6 ve 7 sayıları çıkarılmalıdır. Buna göre, üçüncü kenar uzunluğunun santimetre cinsinden alabileceği değerler 2, 3, 4, 5, 8, 9, 10, 11 ve 12'dir.

CEVAP: C

2015-2016 TEOG

Soru 7: (2015-2016 TEOG 2. Dönem Sınav Sorusu)

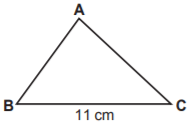
Şekildeki ABC üçgeninin çevresi santimetre cinsinden bir tam sayı ve |BC| = 11 cm’dir.

Buna göre ABC üçgeninin çevresi en az kaç santimetredir?

A) 13

B) 14

C) 21

D) 23

Çözüm:

ABC üçgeninin çevresi, kenar uzunluklarının toplamıdır.

Çevre = |AB| + |AC| + 11

Bir üçgende iki kenar uzunluğunun toplamı, üçüncü kenar uzunluğundan fazla olmalıdır. Buna göre |AB| + |AC| uzunluğu, 11 cm’den büyüktür. Santimetre cinsinden çevre bir tam sayı olduğuna göre, |AB| + |AC|’nin alabileceği en küçük değer 12 cm’dir. Dolayısıyla, üçgenin çevresi en az 11 + 12 = 23 cm'dir.

CEVAP: D

Soru 8: (2015-2016 TEOG 2. Dönem Mazeret Sınav Sorusu)

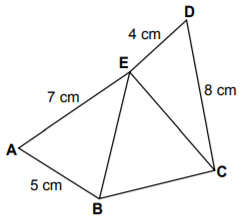
Şekilde verilen ABE ve CDE üçgenlerinde |AB| = 5 cm, |CD| = 8 cm, |DE| = 4 cm, |EA| = 7 cm'dir.

BCE üçgeninin kenar uzunlukları santimetre cinsinden birer tam sayı olduğuna göre bu üçgenin çevresi en az kaç santimetredir?

A) 13

B) 12

C) 11

D) 10

Çözüm:

BCE üçgenindeki kenar uzunluklarının alabileceği en küçük değerleri bulalım.

|BE| :

|BE| uzunluğu, ABE üçgendeki diğer iki kenar uzunluğu arasındaki farktan (7 – 5 = 2 cm'den) büyük olmalıdır. Buna göre |BE|'nin alabileceği en küçük değer 3 cm'dir.

|EC| :

|EC| uzunluğu EDC üçgenindeki diğer iki kenar uzunluğunun farkından (8 – 4 = 4 cm'den) büyük olmalıdır. Dolayısıyla, santimetre cinsinden |EC|'nin alabileceği en küçük tam sayı değeri 5'tir.

|BC| :

|BE| = 3 cm ve |EC| = 5 cm olduğunu varsayarsak, |BC|'nin alabileceği en küçük değer bu iki sayının farkından (5 – 3 = 2 cm'den) büyük olmalıdır. Bu nedenle, seçtiğimiz diğer iki kenar uzunluğunu temel aldığımızda |BC|'nin santimetre cinsinden alabileceği en küçük tam sayı değeri 3 olur.

Çevre Uzunluğu

Yukarıda bulduğumuz değerleri kullanarak çevrenin en az 3 + 5 + 3 = 11 cm olabileceğini görebiliriz.

Not: |BE|'nin uzunluğunu 4 cm olarak seçseydik, |BC| için daha küçük bir değer olan 2 cm'yi kullanabilirdik. Yalnız bu durumda, çevre uzunluğu için yine aynı sonucu elde ederdik.

CEVAP: C

Soru 9: (2015-2016 TEOG 2. Dönem Mazeret Sınavı Sorusu)

Tüm iç açılarının ölçüleri derece cinsinden birer tam sayı olan ABC üçgeninde |AC| < |AB| < |BC| ise ... en fazla kaç derece olabilir?

A) 58

B) 59

C) 60

D) 61

Çözüm:

Bir üçgende büyük açının karşısında uzun kenar ve küçük açının karşısında kısa kenar bulunur.

|AC| < |AB| < |BC| olduğuna göre, açılar arasındaki sıralama ... < ... < ...'dir. Bu üçgendeki en küçük açı ...'dir.

...'nin en büyük değeri için diğer iki açının olası en küçük değerleri alması gerekir. ...'in değerine x dersek, ...'nin değeri en az x + 1 ve ...'nın değeri en az x + 2 olur. Bu üç açının toplamı 3x + 3'tür. Bulduğumuz toplamı 180⁰'ye eşitleyerek ...'nin alabileceği en büyük değeri bulabiliriz.

3x + 3 = 180⁰

⇒ 3x = 177⁰

⇒ x = 59⁰

CEVAP: B

2016-2017 TEOG

Soru 10: (2016-2017 TEOG 2. Dönem Sınav Sorusu)

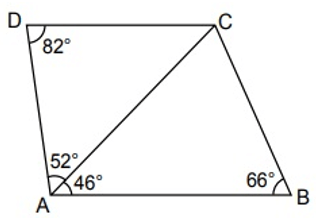
Şekildeki ABCD dikdörtgeninde; ..., ..., ... ve ... dir.

Buna göre aşağıdakilerden en uzunu hangisidir?

A) [AB]

B) [BC]

C) [CD]

D) [DA]

Çözüm:

Önce, şekilde verilmeyen iç açıları bulalım.

... ... ...
... ... ...

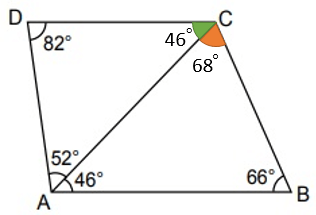
Bir üçgendeki en uzun kenar, en büyük açının karşısındadır.

İç açılarına baktığımızda, ADC üçgenindeki en büyük kenarın [AC] olduğunu görebiliriz.

ABC üçgeninde [AB]'nin karşısındaki açı, [AC]'nin karşısındaki açıdan büyüktür. Bu nedenle [AB]'nin uzunluğu [AC]'ninkinden fazladır. Bu üçgendeki en büyük açı [AB]'nin karşısında olduğu için şekildeki en uzun kenar [AB]'dir.

CEVAP: A

→KONU ANASAYFASINA DÖN←