ÇIKMIŞ SORULAR: ÜÇGENİN KENAR UZUNLUKLARI VE AÇILARI İLE İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-1
Aşağıda, TEOG sınavlarında üçgenin kenar ve açılarıyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2013-2014 TEOG
Bir ABC üçgeninde ...'dir. Buna göre, üçgenin kenarları arasında aşağıdaki hangi ilişki olamaz?
Çözüm:
Bir üçgenin iç açılarından biri 100⁰ ise diğer iki açının toplamı 180⁰ – 100⁰ = 80⁰'dir. Dolayısıyla, bu üçgendeki en büyük açı 100⁰'dir.

Bir ABC üçgeninde ... açısının karşısındaki kenar BC'dir. En büyük açının karşısında en uzun kenar olduğundan bu üçgendeki en uzun kenar BC'dir. Buna göre, |BC| uzunluğu diğer kenar uzunluklarına eşit veya bu uzunluklardan küçük olamaz. D seçeneğinde, |BC| uzunluğu farklı bir kenar uzunluğuna eşitlendiğinden doğru cevap bu seçenektir.
CEVAP: D
Kenar uzunlukları santimetre cinsinden birer tam sayı ve çevresinin uzunluğu 9 cm olan kaç farklı üçgen vardır?
Çözüm:
Soruda verilen şartlara uyan kenar uzunlukları santimetre cinsinden
- 4, 4 ve 1;
- 2, 3 ve 4; veya
- 3, 3 ve 3;
olabilir.
CEVAP: A
2014-2015 TEOG
Kenarlarından ikisinin uzunluğu 8 cm ve 5 cm olan bir üçgenin diğer kenarının uzunluğu aşağıdakilerden hangisi olabilir?
Çözüm:
Üçüncü kenarın uzunluğu, 8 + 5 = 13 cm'den küçük ve 8 – 5 = 3 cm'den büyüktür. Sadece C seçeneğinde verilen uzunluk bu aralıktadır.
CEVAP: C
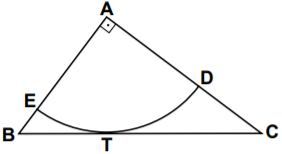
Şekildeki dik üçgende ... dir. [BC] kenarına T noktasında teğet olan A merkezli çember yayı [AC]’nı D noktasında, [AB]’nı E noktasında kesmektedir.
|DC| > |BE| olduğuna göre, ... üçgeninin açılarının ölçülerinin doğru sıralanışı aşağıdakilerden hangisidir?
Çözüm:
Bir dik üçgendeki en büyük açı, dik açıdır. Dolayısıyla, ...'nın değeri diğer iki açı ölçüsünden büyüktür. ... ve ...’den hangisinin daha büyük olduğunu bulabilmek için bu açıların karşılarındaki kenar uzunluklarını karşılaştırabiliriz.
|AE| ve |AD| uzunlukları çemberin yarıçapına eşittir. |DC| > |BE| olduğundan, |AC| uzunluğu |AB|’den büyüktür. Bu nedenle, ... ölçüsü ...'den büyüktür. Doğru sıralama aşağıdaki gibidir.
... < ... < ...
CEVAP: D

Şekildeki ... dik üçgeninde ... ve ...'dir. [AD], ...’nın açıortayı olduğuna göre aşağıdaki doğru parçalarından hangisi en uzundur?
Çözüm:
Bu soruyu çözebilmek için önce şekildeki tüm iç açıları bulmamız gerekiyor. Kenar uzunlukları arasındaki sıralamaları bulabilmek için bu iç açıları kullanıyoruz.
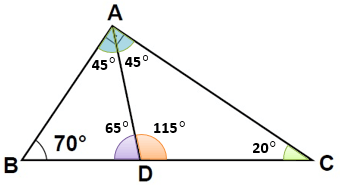
İç Açılar:
... üçgeninin iç açılarından ikisi 70⁰ ve 90⁰'dir. Üçüncü iç açıyı bulabilmek için bu açıların toplamını 180⁰'den çıkarabiliriz.
... ... ...
[AD] açıortay olduğuna göre, hem ... hem de ..., 90⁰'nin yarısına eşittir.
...
... açısının değerini bulabilmek için ... üçgeninde değerini bildiğimiz açıların toplamını 180⁰'den çıkarabiliriz.
... ... ...
... üçgenin iç açılarından ikisinin 45⁰ ve 20⁰ olduğunu gördük. Geriye kalan son kalan açıyı hesaplayabilmek için bu üçgenin iç açıları toplamını 180⁰'ye eşitleyebiliriz.
... ... ...

Şimdi bulduğumuz iç açıları kullanarak, kenar uzunlukları arasındaki büyüklük-küçüklük ilişkilerini elde edelim.
Kenar Uzunlukları:
-
... üçgenindeki en büyük açı ... olduğundan [AB], [BD] ve [AD] doğru parçaları arasındaki en uzun kenar bu açının karşısındaki [AD]’dir.
|AD| > |AB| > |BD|
-
... üçgenindeki en büyük açı ... olduğundan bu üçgendeki en uzun kenar [AC]’dir. Böylece [AD], [DC] ve [AC] doğru parçaları arasından en uzununun [AC] olduğunu görebiliriz. Bu nedenle, cevap B’dir.
|AC| > |DC| > |AD|
CEVAP: B
