ÇIKMIŞ SORULAR: PİSAGOR BAĞINTISIYLA İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-1
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 0 | 3 | 0 | 2 | 1 | 0 | 0 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 0 |
| 2018-2019 | 3 |
| 2019-2020 | 0 |
| 2020-2021 | 2 |
| 2021-2022 | 1 |
| 2022-2023 | 0 |
| 2023-2024 | 0 |
Aşağıda, LGS'de Pisagor bağıntısıyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2018-2019 LGS
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
Geometri tahtası, bir zeminin üzerine eşit aralıklarla yerleştirilmiş çivilerden oluşur.
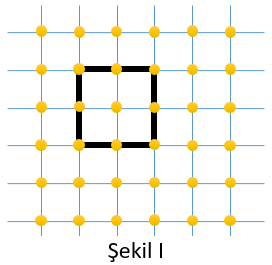
Şekil I’deki geometri tahtasında oluşturulan karenin alanı ... ... birimkaredir.
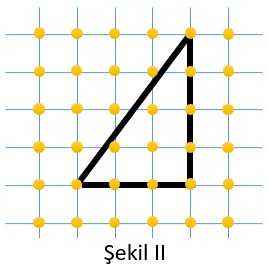
Bu geometri tahtasında Şekil II’deki gibi oluşturulan üçgenin çevre uzunluğu x cinsinden kaç birimdir?
Çözüm:
Şekil I'deki geometri tahtasında oluşturulan karenin alanı ... ... ... birimkaredir. Buna göre, karenin kenar uzunluğu ... ... birimdir.
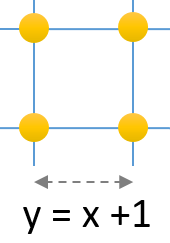
İki komşu çivi arasındaki uzaklık ... ile gösterilirse, karenin kenar uzunluğu ... olur. Bu uzunluk ...'ye eşit olduğu için ... ... birimdir.
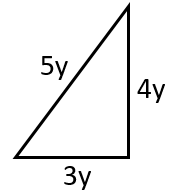
Şekil II'deki üçgenin dik kenar uzunlukları ... ve ... birimdir. Bu üçgende Pisagor Teoremi kullanılarak, hipotenüs uzunluğunun ... olduğu görülebilir.
... ... ... ...
Üçgenin çevresi, kenar uzunluklarının toplamına eşittir.
Üçgenin Çevresi = ... ...
... ifadesinde ... yerine ... yazıldığında, sonucun ... birim olduğu görülebilir.
... ... ...
CEVAP: A
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
ABCD dikdörtgeni biçimindeki bir kâğıt parçasının bir yüzüne aşağıdaki gibi 10 eş dikdörtgen çizilip bu dikdörtgenler boyanıyor.
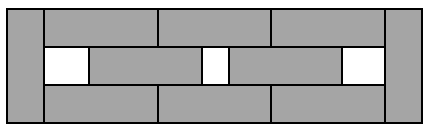
Kâğıdın bu yüzündeki boyanmayan bölgelerin alanları toplamı 30 cm2 olduğuna göre ABCD dikdörtgeninin köşegenlerinden birinin uzunluğu kaç santimetredir?
Çözüm:
Boyasız alan:
Orta kısımdaki boyanmayan bölgelerin toplam alanı, eş dikdörtgenlerden birinin alanına eşittir. Bu durum, orta kısımdaki iki dikdörtgenin sola ve sağa yaslanmasıyla da görülebilir.

Eş dikdörtgenlerin kenar uzunlukları:

Eş dikdörtgenlerin kısa kenar uzunluğu ... ile ifade edildiğinde uzun kenar ... çıkar. Buna göre, boyasız bölgenin alanı ... cm2'dir. ... ifadesi 30'a eşitlenerek ...'in ...'a eşit olduğu görülebilir.
...
⇒ ...
⇒ ... cm
Kağıdın kenar uzunluğu:

- Kısa Kenar: ... cm
- Uzun Kenar: ... ... ... cm
Köşegen uzunluğu:
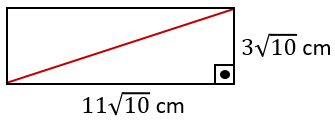
İki komşu kenar ve köşegen bir dik üçgen oluşturur. Bu dik üçgenin hipotenüsü, kağıdın köşegenidir. Köşegen uzunluğunun karesi Pisagor Teoremi'ne göre dik kenar uzunluklarının karelerinin toplamına eşittir.
...
...
... cm2
Buna göre köşegen uzunluğu ... cm'dir.
CEVAP: C
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
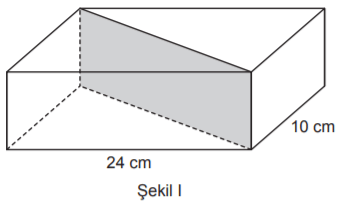
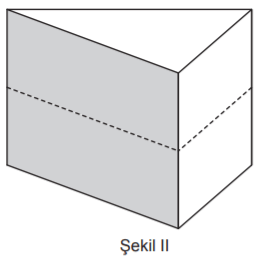
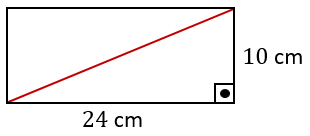
Taban ayrıtlarının uzunlukları 10 cm ve 24 cm olan dikdörtgenler prizması biçimindeki tahta blok Şekil I’deki gibi taban köşegenleri boyunca tabanlara dik olacak şekilde kesilerek iki eş parçaya ayrılıyor. Elde edilen iki parça üst üste yapıştırılarak Şekil II’deki dik üçgen dik prizma biçiminde bir tahta blok oluşturuluyor.
Elde edilen dik üçgen dik prizma ile başlangıçta verilen dikdörtgenler prizmasının ayrıtlarının uzunlukları toplamı birbirine eşittir.
Buna göre dikdörtgenler prizması şeklindeki tahta bloğun yüksekliği kaç santimetredir?
Çözüm:
Dikdörtgenler Prizması:
Dikdörtgenler prizmasının yüksekliği x ile ifade edildiğinde, ayrıt uzunluklarının toplamı 4(24 + 10 + x) = 136 + 4x cm olur.
Dik Üçgen Dik Prizma:
Pisagor Teoremi kullanılarak, dikdörtgenler prizmasının taban köşegeninin 26 cm olduğu görülebilir.
... ... ... cm
Buna göre, dik üçgen dik prizmanın ayrıt uzunluklarının toplamı 2(26 + 10 + 24) + 3 . 2x = 120 + 6x cm'dir.
Denklem:
x cinsinden bulunan ifadeler eşitlendiğinde aşağıdaki denklem elde edilir.
136 + 4x = 120 + 6x
⇒ 136 – 120 = 6x – 4x
⇒ 16 = 2x
⇒ x = 8 cm
Buna göre, dikdörtgenler prizmasının yüksekliği 8 cm'dir.
CEVAP: A
2020-2021 LGS
Dik üçgenlerde, 90⁰ lik açının karşısındaki kenara hipotenüs denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

Kenarlarının uzunlukları x cm ve 3x cm olan dikdörtgen şeklindeki karton ile bir yüzünün alanı 80 cm2 olan kare şeklindeki kâğıt aşağıda verilmiştir.
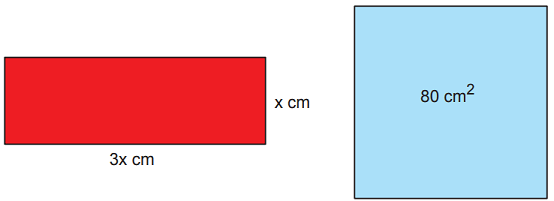
Bu karton ve kâğıt üst üste yerleştirildiğinde ikişer köşeleri aşağıdaki gibi çakışmaktadır.
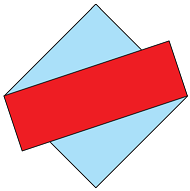
Buna göre dikdörtgen şeklindeki kartonun çevresinin uzunluğu kaç santimetredir?
Çözüm:
Alanı 80 cm2 olan karenin kenar uzunluğu ... cm'dir. Bu karenin köşegen uzunluğunu bulabilmek için Pisagor bağıntısını kullanabiliriz.
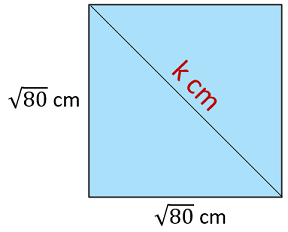
... ... ... cm2
⇒ ... cm
Bu uzunluk aynı zamanda kırmızı dikdörtgene ait köşegenin de uzunluğudur. Bu bilgiyi ve Pisagor bağıntısını kullanarak x'in değerini elde edebiliriz.
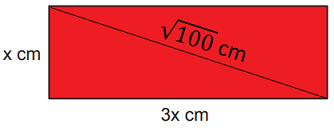
...
⇒ ...
⇒ ...
⇒ ...
⇒ ...
Buna göre, kırmızı dikdörtgenin çevre uzunluğu
... ... ... ... cm'dir.
CEVAP: A
Eğim, dikey uzunluğun yatay uzunluğa oranıdır.
Dik üçgenlerde, 90⁰ lik açının karşısındaki kenara hipotenüs denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

Bir parkın girişi için yapılacak kapı aşağıda modellenmiştir.

Kapının yapımı için her birinin uzunluğu 100 cm olan altı adet demir çubuk modeldeki gibi uç uca eklenecektir. Modelde verilen dikey doğru, genişliği 352 cm olan bu kapıyı iki eş parçaya bölmektedir. Modele göre 1. cubuk yere dik konumdadır ve 2. çubuğun eğimi %75'tir.
Buna göre 3. çubuğun eğimi kaçtır?
Çözüm:
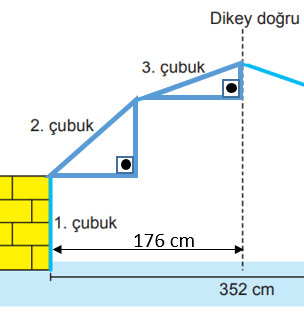
Hipotenüslerinde 2. ve 3. çubuklar olan tabanı yere paralel iki dik üçgen vardır. Bu üçgenlerin taban uzunluklarının toplamı kapının genişliğinin yarısına eşittir.
352 ÷ 2 = 176 cm
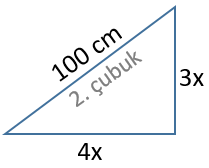
İkinci çubuğun eğimi %75 = ... olduğundan bu çubukla oluşturulan üçgenin yüksekliğini 3x ve taban uzunluğunu 4x ile gösterebiliriz. Bu durumda hipotenüsün uzunluğu 5x olur.
(3x)2 + (4x)2 = (5x)2
Hipotenüsün boyu 100 cm olduğu için x = 100 ÷ 5 = 20 cm'dir. Buna göre taban uzunluğu 4x = 80 cm'dir.
2. ve 3. çubukların oluşturduğu üçgenlere ait tabanların toplam uzunluğu 176 cm olduğundan 3. çubuğa ait üçgenin tabanı 176 – 80 = 96 cm uzunluğundadır.

Tabanı 96 cm ve hipotenüsü 100 cm olan dik üçgenin yüksekliği 28 cm'dir.
y2 + (96)2 = (100)2
⇒ y2 = 784
⇒ y = 28 cm
Buna göre, 3. çubuğun eğimi ...'e eşittir.
CEVAP: A
