ÇIKMIŞ SORULAR: PİSAGOR BAĞINTISIYLA İLGİLİ ÇIKMIŞ TEOG SORULARI VE ÇÖZÜMLERİ-2
Aşağıda, TEOG sınavlarında Pisagor bağıntısıyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki sayfaya geçebilirsiniz.
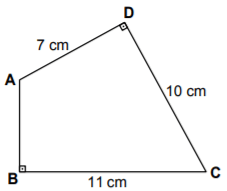
Şekildeki ABCD dikdörtgeninde [AB] ⊥ [BC] ve [AD] ⊥ [DC]'tir.
|AD| = 7 cm, |DC| = 10 cm ve |CB| = 11 cm olduğuna göre |AB| kaç santimetredir?
Çözüm:
A ve C noktalarını birleştiren bir doğru parçası çizdiğimizde iki dik üçgen elde ederiz: ADC ve ABC

|AC| uzunluğunu hesaplayabilmek için ADC üçgeninde Pisagor bağıntısını kullanabiliriz.
|AC|2 = |AD|2 + |DC|2 = 72 + 102 = 49 + 100 = 149 cm2
|AC|2 değerini, ABC üçgeni için kurduğumuz Pisagor bağıntısında yerine yazarak, |AB| uzunluğunu elde edebiliriz.
|AC|2 = |AB|2 + |BC|2
⇒ 149 = |AB|2 + 112
⇒ |AB|2 = 149 – 121
⇒ |AB|2 = 28
⇒ |AB| = ... cm
CEVAP: A
2016-2017 TEOG
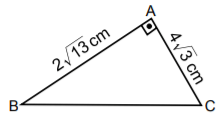
Şekilde verilen ABC dik üçgeninde [AB] ... [AC]'dir.
|AB| = ... cm ve |AC| = ... cm olduğuna göre |BC| kaç santimetredir?
Çözüm:
|BC| uzunluğunu hesaplayabilmek için Pisagor bağıntısını kullanabiliriz.
...
...
...
...
...
... cm
CEVAP: D

ABC ikizkenar üçgeninde |AB| = |AC| ve [AD] ... [BC]'tir.
|BC| = 16 cm ve |AB| = 17 cm olduğuna göre |AD| kaç santimetredir?
Çözüm:
|AB| = |AC| olduğu için [AD] yalnızca yükseklik değil aynı zamanda kenarortaydır ve [BC] kenarını iki eşit parçaya böler. Bu nedenle |BD| = 8 cm'dir. ABD dik üçgeninde Pisagor bağıntısını kullanarak |AD| uzunluğunu elde edebiliriz.
|AB|2 = |BD|2 + |AD|2
⇒ 172 = 82 + |AD|2
⇒ 289 = 64 + |AD|2
⇒ 225 = |AD|2
⇒ |AD| = 15 cm
CEVAP: B
