ÇIKMIŞ SORULAR: KONUYLA İLGİLİ ÇIKMIŞ SORULAR VE ÇÖZÜMLERİ

Aşağıda, 2013 yılından bu yana liselere giriş sınavlarında yükseklik, kenarortay ve açıortayla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz.

(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)

2013-2014 TEOG

Soru 1: (2013-2014 TEOG 2. Dönem Sınav Sorusu)

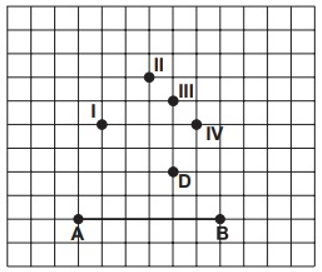
Verilen şekle göre, hangi nokta C köşesi olarak seçilirse ABC üçgeninin AB kenarına ait kenarortayı D noktasından geçer?

A) I

B) II

C) III

D) IV

Çözüm:

AB kenarına ait kenarortay, bu doğru parçasının orta noktasından geçer. Hem AB'nin orta noktasından hem de D noktasından geçen bir doğru çizdiğimizde, bu doğrunun aynı zamanda IV noktasından da geçtiğini görebiliriz. Bu nedenle C noktası IV olabilir.

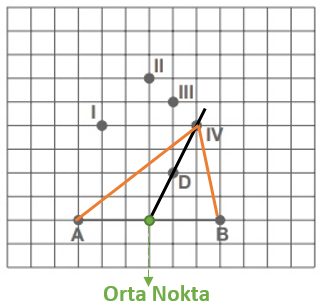
CEVAP: D

2015-2016 TEOG

Soru 2: (2015-2016 TEOG 1. Dönem Sınav Sorusu)

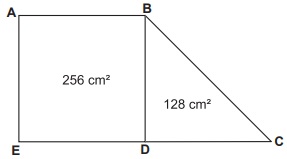
2015-2106 teog yükseklikle ilgili çıkmış soru

Şekildeki ABDE karesinin alanı 256 cm² ve BCD dik üçgeninin alanı 128 cm² dir.

Buna göre |EC| kaç santimetredir?

A) 20

B) 24

C) 28

D) 32

Çözüm:

EC doğru parçası 2 bölümden oluşmaktadır: ED ve DC

|ED|

ABDE karesinin alanı 256 cm² olduğundan kenar uzunğu ... cm'dir.

|ED| = 16 cm

|DC|

BCD dik üçgeninin alanı 128 cm² ve yüksekliği 16 cm'dir. Buna göre taban uzunluğu |DC| = ... cm'dir.

Toplam

EC'nin uzunluğu, ED ve DC'nin uzunluklarının toplamına eşittir.

|EC| = |ED| + |DC| = 16 + 16 = 32 cm

CEVAP: D

Soru 3: (2015-2016 TEOG 2. Dönem Sınav Sorusu)

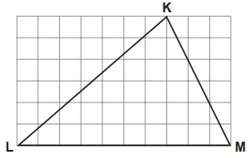
Kareli zeminde verilen KLM üçgeninde [LM] kenarına ait kenarortayın ve yüksekliğin [LM] kenarını kestiği noktalar arasındaki uzaklık 12 cm'dir.

Buna göre |LM| kaç santimetredir?

A) 48

B) 60

C) 72

D) 84

Çözüm:

[LM] kenarına ait yüksekliğin ve kenarortayın bu kenarı kestiği noktalar arasındaki uzaklık 2 birimdir. 2 birim 12 cm'ye eşitse, 1 birim 6 cm'dir. Buna göre, 10 birimlik |LM| uzunluğu 10 × 6 cm = 60 cm'dir.

CEVAP: B

2016-2017 TEOG

Soru 4: (2016-2017 TEOG 2. Dönem Sınav Sorusu)

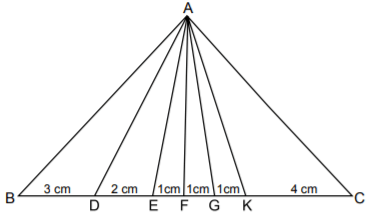
Yukarıdaki ABC üçgeninde BC kenarı üzerinde ayrılan parçaların uzunlukları verilmiştir.

|AB| = |AC| olduğuna göre ABC üçgeninin BAC açısına ait açıortayı aşağıdakilerden hangisidir?

A) [AE]

B) [AF]

C) [AG]

D) [AK]

Çözüm:

|AB| ve |AC| uzunlukları aynı olduğuna göre ABC bir ikizkenar üçgendir ve BAC açısına ait açıortay aynı zamanda BC kenarına ait kenarortaydır. Kenarortay, ait olduğu kenarı ikiye böler. BC kenarının orta noktası F'dir. Buna göre ABC üçgeninin kenarortayı ve dolayısıyla açıortayı [AF] doğru parçasıdır.

CEVAP: B

Soru 5: (2016-2017 TEOG 2. Dönem Mazeret Sınavı Sorusu)

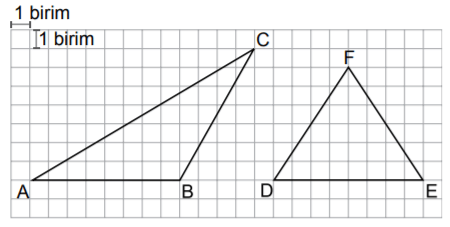
2016-2017 üçgende yükseklik, kenarortay ve açıortay sorusu

Yukarıdaki kareli zeminde verilen ABC üçgeninde, AB kenarına ait yükseklik ile DEF üçgenindeki F açısına ait açıortayın uzunlukları toplamı kaç birimdir?

A) 13

B) 10

C) 9

D) 6

Çözüm:

DEF üçgeninde DE kenarına bir dik indirdiğimizde, bu doğru parçasının DE'yi 2 eşit parçaya böldüğünü görebiliriz. Bu da bize DEF üçgeninde yüksekliğin aynı zamanda kenarortay olduğunu gösterir. Buradan DEF'nin ikizkenar olduğunu çıkarabiliriz. Bu üçgende DE kenarına ait yükseklik aynı zamanda F açısına ait açıortaydır.

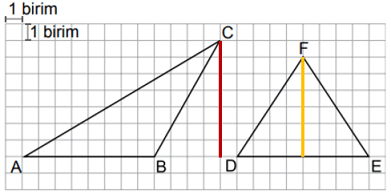
Yukarıda ABC üçgeninde AB kenarına ait yüksekliği kırmızı ve DEF üçgeninde DE kenarına ait yüksekliği sarı doğru parçaları ile gösteriyoruz. Kırmızı doğru parçası 7 birim ve sarı doğru parçası 6 birim olduğu için toplam uzunluk 7 + 6 = 13 birimdir.

CEVAP: A

→KONU ANASAYFASINA DÖN←