TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ EŞKENAR ÜÇGEN
TEOREMLER VE İSPATLAR
EŞKENAR ÜÇGENDE YÜKSEKLİK, KENARORTAY VE AÇIORTAY EŞLİĞİ
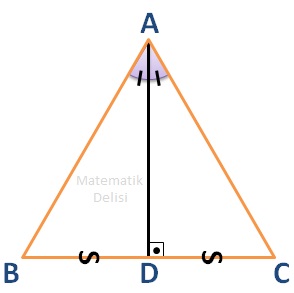
📚 Eşkenar üçgende bir kenara ait yükseklik aynı zamanda hem kenarortay hem de açıortaydır.
İSPAT
YÜKSEKLİK = AÇIORTAY
Bir ... eşkenar üçgeni tanımlayıp, BC kenarına ait yüksekliği çizelim.
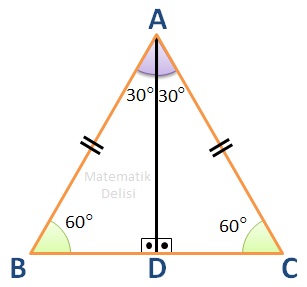
Eşkenar üçgenlerde tüm iç açılar 60⁰ olduğu için A köşesinden indirdiğimiz yükseklik ile AC kenarı arasında kalan açı
... ...
...
...
çıkar. Benzer şekilde ... açısının da 30⁰ olduğunu bulabiliriz.
... ...
...
...
... ve ... açıları aynı olduğu için BC kenarına indirdiğimiz dik, aynı zamanda ... açısının açıortayıdır.
YÜKSEKLİK = KENARORTAY
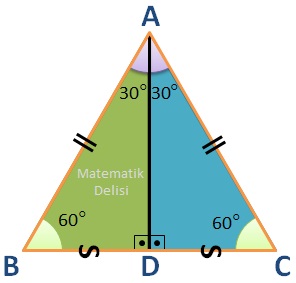
... ve ... üçgenlerinin tüm iç açıları aynı olduğu için bu üçgenler benzerdirler. Ayrıca, AD kenarı her iki üçgen için de ortak olduğu için bu üçgenler aynı zamanda eş üçgenlerdir. Eş üçgenlerde eş açıların karşısındaki kenarlar eşit uzunlukta oldukları için 30⁰'nin karşısındaki BD ve DC kenarlarının uzunlukları eşittir.
|BD| = |DC|
Bu eşitlik, AD doğru parçasının BC kenarına ait kenarortay olduğunu gösterir.
TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ EŞKENAR ÜÇGEN