BÖLÜM 5: ÖZEL ÜÇGENLERDE YÜKSEKLİK, KENARORTAY VE AÇIORTAY

EŞKENAR ÜÇGENDE AÇIORTAY, KENARORTAY VE YÜKSEKLİK

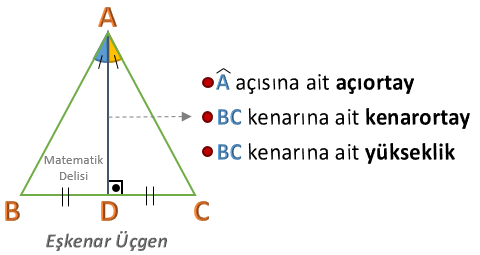
eşkenar üçgende açıortay, kenarortay ve yükseklik

Bir eşkenar üçgenin kenarortayı, aynı zamanda bu üçgenin açıortayı ve yüksekliğidir. (Nedenini öğrenmek için tıklayın.)

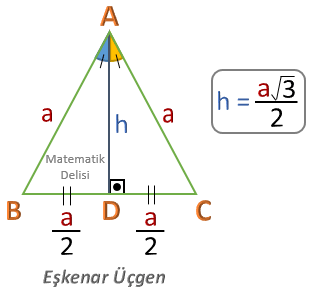
Kenar uzunluğu ... birim olan eşkenar üçgenin yüksekliği ... birimdir. Pisagor teoremini kullanarak bu sonucu kolayca elde edebiliriz.

...

⇒ ...

ÖRNEK:

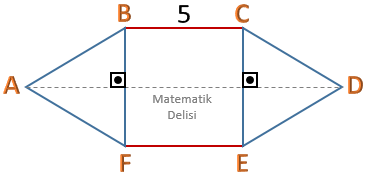
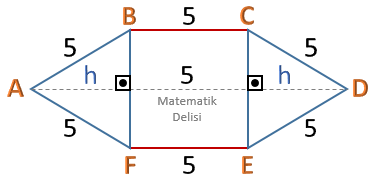
Yukarıdaki şekilde ABF ve CED birer eşkenar üçgen ve BCEF bir karedir. |BC| uzunluğu 5 birim olduğuna göre, |AD| kaç birimdir?

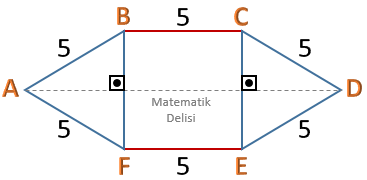
Şekildeki karenin ve üçgenlerin kenar uzunlukları 5 birimdir.

AD doğru parçası yukarıdaki gibi üç parçaya ayrılabilir. Bu parçalardan ikisi üçgenlerin yüksekliğidir. Üçüncü parçanın uzunluğu ise karenin kenar uzunluğuna eşittir. Eşkenar üçgenin yüksekliği ... birime ve karenin kenar uzunluğu ... birime eşit olduğundan, |AD| uzunluğu

|AD| = ... ... birimdir.

Kenar uzunluğu ... birim olan bir eşkenar üçgenin alanı ... birim²'dir.

İKİZKENAR ÜÇGENDE AÇIORTAY, KENARORTAY VE YÜKSEKLİK

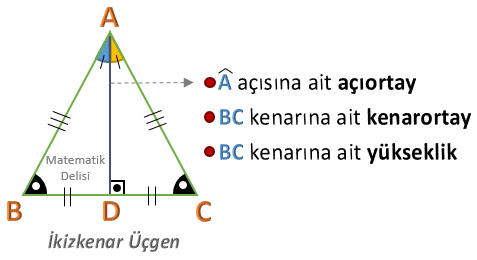
İkizkenar üçgende yükseklik, kenarortay ve açıortay

İkizkenar üçgende eş kenarların kesişim noktasındaki açıya ait olan açıortay, aynı zamanda hem kenarortay hem de yüksekliktir. (Nedenini görmek için buraya tıklayın.)

ÖRNEK:

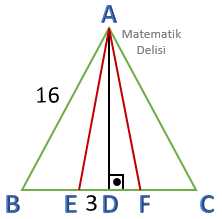
ABC bir eşkenar üçgendir. |AE| = |AF|, |AB| = 16 birim ve |ED| = 3 birim olduğuna göre FC doğru parçasının uzunluğu kaç birimdir?

|AE| ve |AF| uzunluklarının eşit olması AEF üçgeninin ikizkenar olduğunu gösterir. AD doğru parçası, hem ABC hem de AEF üçgenlerinin yüksekliğidir. İkizkenar üçgende ikiz olmayan kenara ait yükseklik aynı zamanda kenarortay olduğundan |DF| = |ED| = 3 birimdir. Ayrıca, ABC bir eşkenar üçgen olduğundan BC doğru parçası 16 birim uzunluğundadır.

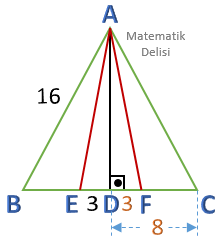
ABC eşkenar olduğu için AD doğru parçası aynı zamanda bu üçgenin de kenarortayıdır. Başka bir deyişle, D noktası AB doğru parçasını 2 eşit parçaya böler. Dolayısıyla, |DC| uzunluğu 8 birime eşittir. |DC| = 8 ve |DF| = 3 olduğundan, |FC| uzunluğu 5 birimdir.

|FC| = |DC| – |DF| = 8 – 3 = 5 birim

→KONU ANASAYFASINA DÖN←