İSPAT

YÜKSEKLİK = AÇIORTAY

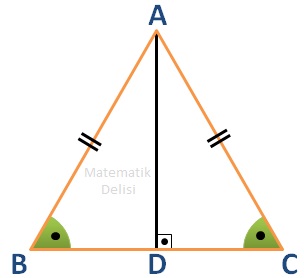
İkizkenar bir üçgende ikiz olmayan kenara ait yüksekliği çizelim. Oluşan ... ve ... üçgenlerinde iç açılardan ikisi aynı olduğu için bu üçgenlerin üçüncü açılarının da aynı olması gerekir.

• ... ...,
• ... ... ve
• ... ....

AD yüksekliği ... açısını iki eşit parçaya böldüğü için aynı zamanda açıortaydır.

YÜKSEKLİK = KENARORTAY

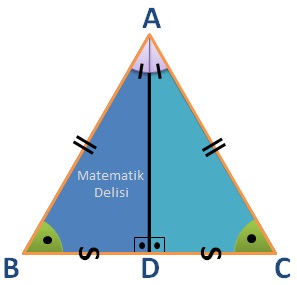
... ve ... üçgenlerinin tüm iç açıları eşit olduğundan bu üçgenler benzerdir. Ayrıca, bu iki dik üçgenin hipotenüsleri eşit uzunluklarda olduğu için aynı zamanda eştir. Eş üçgenlerde kenar uzunlukları da eşit olacağından |BD| uzunluğunun |DC|'ye eşit olduğunu söyleyebiliriz. Bu da, AD yüksekliğinin BC'yi 2 eşit parçaya böldüğünü ve BC'ye ait kenarortay olduğunu gösterir.