BÖLÜM 4: ÜÇGENİN ALANI
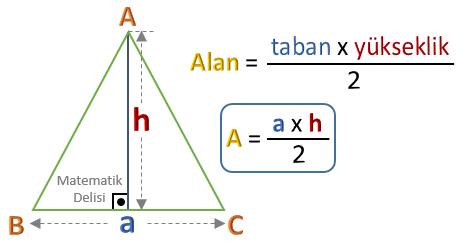
![]() Üçgenin alanı, taban uzunluğuyla yüksekliğin çarpımının yarısına eşittir.
(Nedenini görmek için tıklayın.)
Üçgenin alanı, taban uzunluğuyla yüksekliğin çarpımının yarısına eşittir.
(Nedenini görmek için tıklayın.)

Yukarıdaki taralı bölgenin alanını bulalım.
Taralı bölgenin alanı, ... ve
... üçgenlerinin alanları arasındaki farka eşittir. İki üçgenin de
tabanları
... üçgeninin alanı
... birim2 ve
... üçgeninin alanı
... birim2'dir.
Taralı bölgenin alanı ise, 20 – 7,5 = 12,5 birim2'dir.

![]() Üçgenin alanı hesaplanırken, herhangi bir kenar uzunluğu ve bu kenara ait yükseklik kullanılabilir.
Aşağıdaki formüllerin tümü yukarıdaki üçgenin alanını verir.
Üçgenin alanı hesaplanırken, herhangi bir kenar uzunluğu ve bu kenara ait yükseklik kullanılabilir.
Aşağıdaki formüllerin tümü yukarıdaki üçgenin alanını verir.
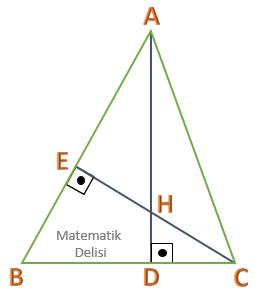
Yukarıdaki üçgende |AD| = 10 birim, |BC| = 8 birim ve |AB| = 12 birim olduğuna göre, |EC| uzunluğu kaç birimdir?
ABC üçgeninin alanı
... ... birim2'dir.
Bu alan, aynı zamanda
... ... ... birim2'ye
eşittir. Alan için elde ettiğimiz ifadeleri birbirine eşitleyerek |
...
⇒ ... ... birim
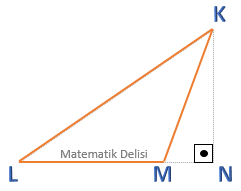
![]() Tabanla yüksekliğin kesişmediği durumlarda da aynı alan formülü geçerlidir. Örneğin, yukarıdaki üçgenin
alanı ...'dir.
Tabanla yüksekliğin kesişmediği durumlarda da aynı alan formülü geçerlidir. Örneğin, yukarıdaki üçgenin
alanı ...'dir.
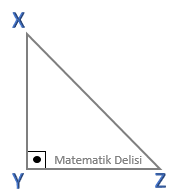
![]() Dik üçgenlerde, dik kenarlardan biri, diğerinin yüksekliğidir. Buna göre, dik üçgenin alanı dik kenar
uzunluklarının çarpımının yarısına eşittir. Örneğin, yukarıdaki
... üçgeninin alanı
...'dir.
Dik üçgenlerde, dik kenarlardan biri, diğerinin yüksekliğidir. Buna göre, dik üçgenin alanı dik kenar
uzunluklarının çarpımının yarısına eşittir. Örneğin, yukarıdaki
... üçgeninin alanı
...'dir.
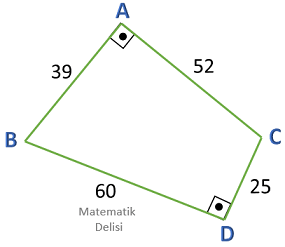
Kenar uzunlukları verilen yukarıdaki dörtgenin alanını bulalım.
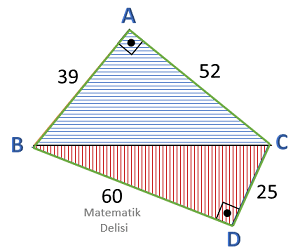
Dörtgenin alanı bu üçgenlerin alanlarının toplamıdır. ... üçgeninin alanı
... birim2
ve ... üçgeninin alanı
... birim2
olduğundan, dörtgenin toplam alanı ... birim2'ye eşittir.
