İSPAT

Üçgenin yükseklik formülünün tüm üçgenler için doğru olduğunu 3 aşamada ispatlayacağız.

1. Aşama : Dik üçgenler

Dik üçgenlerde alan formülünü ispatlayabilmek için dikdörtgenin alan formülünü ve üçgenlerde eşliği kullanıyoruz.

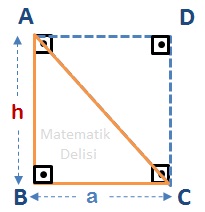
Dik üçgeni kullanarak bir dikdörtgen oluşturabilmek için A ve C köşelerinden sırasıyla tabana ve yüksekliğe paralel doğru parçaları çizelim. Böylece kenar uzunlukları ... ve ... olan bir dikdörtgen elde ediyoruz. Oluşturduğumuz dikdörtgenin alanı, iki kenar uzunluğunun çarpımına eşittir.

Bir dikdörtgende karşılıklı kenarların eşit uzunluklarda olduklarını hatırlayalım. Buna göre, DC kenarının uzunluğu ...'ye ve AD kenarının uzunluğu ...'ya eşit olur. Dikdörtgenin içindeki ... ve ... üçgenlerine baktığımızda, kenar uzunluklarının aynı olduğunu görebiliriz.

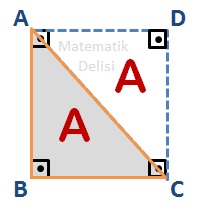
Kenar uzunlukları eşit olan üçgenler eş üçgenlerdir ve eş üçgenlerin alanları da eşittir. ... üçgeninin alanına ... dersek, ... üçgeninin alanı da ... olur. Dikdörtgenin alanı ... ve ...'nin alanlarının toplamına eşittir.

...'yı ilk bulduğumuz alan formülüne eşitlersek,

sonucuna ulaşırız. ... üçgeninin alanı ...'ya eşit olduğundan, bir dik üçgenin alanının tabanı ile yüksekliğinin çarpımının yarısına eşit olduğunu görebiliriz.

... formülünün tüm üçgenler için eşit olduğunu ispatlayabilmek için tabanın yükseklikle kesiştiği ve kesişmediği durumların her ikisini de incelememiz gerekiyor. Sonraki iki aşamada bu durumların ispatını yapıyoruz.

2. Aşama: Yüksekliğin taban ile kesiştiği durum

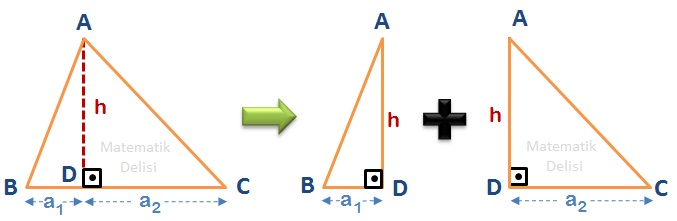
Bir üçgende yükseklik, taban ile kesişiyorsa, bu üçgeni iki dik üçgenin birleşimi gibi düşünebiliriz. Örneğin, yukarıdaki ... üçgeninini ... ve ...'nin AD kenarında birleştirilmiş hali olarak düşünebiliriz. 1. aşamada dik üçgenler için bulduğumuz formülü ... üçgeni için uyguladığımızda, bu üçgenin alanının ... olduğunu ve aynı formülü ... üçgeni için uyguladığımızda ise, alanın ... olduğunu buluruz. ... üçgeninin alanı, ... ve ... üçgenlerinin alanlarının toplamına eşittir.

Yukarıdaki eşitliğin sağ tarafındaki ... ifadesi ... üçgeninin tabanına ve ... ise bu tabana ait yüksekliğe eşit olduğundan, yüksekliği tabanı ile kesişen üçgenlerde üçgenin alan formülünün geçerli olduğunu görebiliriz.

3. Aşama: Yükseliğin tabanın uzantısı ile kesiştiği durum

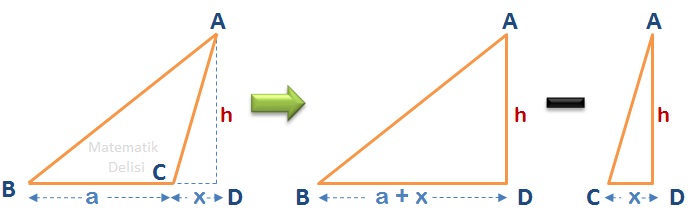
Yüksekliğin tabanın uzantısı ile kesiştiği bir ... üçgeni düşünelim. Bu üçgenin alanı ... ve ... üçgenlerinin alanlarının farkına eşittir. Dik üçgenler için elde ettiğimiz alan formülünü kullanarak ... üçgeninin alanının ...'ye ve ... üçgeninin alanının ...'ye eşit olduğunu çıkarabiliriz. Bu iki ifadenin farkını aldığımızda ... üçgeninin alanı yine taban ile yüksekliğin çarpımının yarısı çıkar.