ÇIKMIŞ SORULAR: ÜSLÜ SAYILARLA İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLER-7
Üslü sayılarla işlemler konusuyla ilgili LGS'de (Liselere Giriş Sınavında) çıkan soruları ve bu soruların çözümlerini aşağıda bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 0 | 1 | 2 | 1 | 1 | 1 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 0 |
| 2018-2019 | 1 |
| 2019-2020 | 2 |
| 2020-2021 | 1 |
| 2021-2022 | 1 |
| 2022-2023 | 1 |
| 2023-2024 | 1 |
2018-2019 LGS
... ≠ ... ve ..., ... tam sayılar olmak üzere
... ve ...
...
Aşağıda sadece ön yüzlerinde birer üslü ifadenin yazılı olduğu 4 mavi ve 4 kırmızı kart verilmiştir.
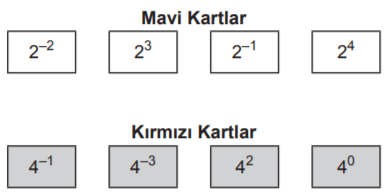
Mavi kartlardaki her bir üslü ifade kırmızı kartlardaki kendisine denk olmayan her bir üslü ifade ile birer kez çarpılarak yeni üslü ifadeler elde ediliyor.
Elde edilen bu üslü ifadelerden ikisinin birbirine oranı en çok kaçtır?
Çözüm:
Kırmızı kartlardaki sayıları da 2 tabanında yazalım.
- 4–1 = (22)–1 = 22 . (–1) = 2–2
- 4–3 = (22)–3 = 22 . (–3) = 2–6
- 42 = (22)2 = 22 . 2 = 24
- 40 = (22)0 = 22 . 0 = 20
En büyük oranı yakalayabilmek için öncelikle çarpma sonucunda elde edilebilecek en küçük ve en büyük sayıları bulmamız gerekir.
En küçük çarpım:
Mavi ve kırmızı kartlardaki en küçük sayılar sırasıyla 2–2 ve 2–6'dır. Bu sayıların çarpımı elde edebileceğimiz en küçük sonucu verir.
2–2 . 2–6 = 2–2 – 6 = 2–8
En büyük çarpım:
Hem mavi hem de kırmızı kartlardaki en büyük sayı 24'tür. Yalnız denk olmayan üslü ifadeler çarpıldığı için 24'ü bu kartlardaki en büyük ikinci sayı ile çarpmamız gerekir. En büyük ikinci sayı 23 olduğundan, elde edilebilecek en büyük çarpım sonucu 24 . 23 = 27'dir.
En büyük oran:
En büyük oranı bulabilmek için en büyük çarpım sonucunu en küçük çarpım sonucuna böleriz.
... ...
CEVAP: B
2019-2020 LGS
... ve ..., ... tam sayılar olmak üzere
... ve ... dir.
Bir kenarının uzunluğu 54 cm olan kare şeklindeki kâğıdın bir yüzüne aşağıdaki gibi 12 eş dikdörtgen ve 1 kare çizilmiştir. Bu şekillerden kare ve 2 eş dikdörtgen kırmızıya boyanmıştır

Buna göre kırmızı bölgelerin alanları toplamı kaç santimetrekaredir?
Çözüm:
Dikdörtgenin kısa kenar uzunluğuna x dersek
- Kırmızı karenin kenar uzunluğu 2x ve
- Kâğıdın yüksekliği 10x olur.
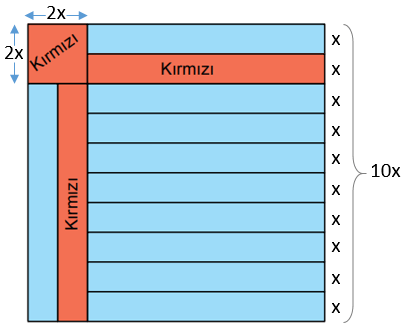
Soruda kare şeklinde olduğu belirtildiği için kâğıdın genişliği de 10x'tir. Buna göre dikdörtgenin uzun kenarı 10x – 2x = 8x'tir.

Santimetrekare cinsinden karenin alanı (2x)2 = 4x2 ve dikdörtgenin alanı x . 8x = 8x2'dir. Dolayısıyla, boyalı bölgelerin toplam alanı santimetrekare cinsinden
4x2 + 2 . 8x2 = 20x2'dir.
10x'i 54'e eşitleyerek x'in değerini bulabiliriz.
10x = 54
⇒ x = ... cm
20x2 ifadesinde x'in değerini yerine yazdığımızda 57 sonucunu elde ederiz.
20x2 = ... = 5 . 56 = 57 cm2
CEVAP: B
... ve ..., ... tam sayılar olmak üzere
... ve ...
...
Bir fabrikada üretilen mavi ve kırmızı renkli otomobiller bir galeriye iki tır ile taşınmaktadır.
Bu otomobillerin birer adedinin kütleleri Tablo 1’de, tırların taşıdığı otomobillerin sayıları Tablo 2’de gösterilmiştir.


A tırı ile taşınan mavi ve kırmızı otomobillerin sayıları birbirine eşittir
İki tırın taşıdığı otomobillerin toplam kütlesi 214 kg olduğuna göre A tırı ile taşınan otomobil sayısı kaçtır?
Çözüm:
Mavi otomobilllerin kütlesini 2 tabanında 45 = (22)5 = 210 kg şeklinde ifade edebiliriz.
A tırı ile taşınan mavi otomobillerin sayısını n ile gösterdiğimizde bu tırda taşınan toplam kütle
n . 210 + n . 211 = n . 210 + 2n . 210 = 3n . 210 kg
olur. B tırında taşınan toplam kütle ise
4 . 210 + 3 . 211 = 4 . 210 + 6 . 210 = 10 . 210 kg'dır.
A ve B tırlarının taşıdığı toplam kütle
3n . 210 + 10 . 210 = (3n + 10) . 210 kg'dır.
Bu kütleyi 214 kg'a eşitleyerek n sayısını bulabiliriz.
(3n + 10) . 210 = 214
⇒ (3n + 10) . 210 = 24 . 210
⇒ 3n + 10 = 24
⇒ 3n + 10 = 16
⇒ 3n = 6
⇒ n = 2
Buna göre A tırında taşınan otomobil sayısı 2 + 2 = 4'tür.
CEVAP: B
2020-2021 LGS
Aşağıdaki tabloda Ordu, Giresun ve Trabzon şehirlerini ziyaret eden turistlerin sayıları verilmiştir.
Tablo: Şehirleri Ziyaret Eden Turistlerin Sayıları
| Şehirler | Turist Sayısı |
| Ordu | 0,125 . 106 |
| Giresun | 9,5 . 104 |
| Trabzon | x . 107 |
Trabzon'u ziyaret eden turistlerin sayısı, Ordu'yu ziyaret eden turistlerin sayısından az ve Giresun'u ziyaret eden turistlerin sayısından fazladır.
Buna göre x'in alabileceği değerlerden biri aşağıdakilerden hangisidir?
Çözüm:
Ordu'yu ziyaret eden turist sayısı
0,125 . 106 = 125 000 ve
Giresun'u ziyaret eden turist sayısı
9,5 . 104 = 95 000'dir.
Trabzon'u ziyaret eden turist sayısı ise 95 000 ile 125 000 arasındadır. x sayısı 10–2 değerini aldığında x . 107 ifadesi istenilen aralıkta çıkar.
CEVAP: C
2021-2022 LGS
a ≠ 0, b ≠ 0 ve k, m, n tam sayılar olmak üzere
(an)m = an . m ve (a . b)k = ak . bk dir.

Yukarıda verilen dokuz adet kutudan her birine bir üslü ifade yazılmıştır. Bu üslü ifadelerden birbirine denk olanların bulunduğu kutular aynı renge boyanacaktır.
Buna göre, boyanmayan kutudaki üslü ifade aşağıdakilerden hangisidir?
Çözüm:
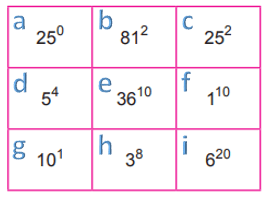
Üslü sayılarla ilgili tanımları ve soruda verilen eşitlikleri kullanarak kutulardaki ifadelere denk sayılar ve ifadeler elde edelim.
g) 101 = 10
Yukarıdaki eşitliklere göre
a ilef ,b ileh ,c iled vee ilei
birbirine denktir. Diğerlerinden herhangi birine denk olmayan tek ifade 101'dir.
CEVAP: D
