ÇIKMIŞ SORULAR: KONUYLA İLGİLİ ÇIKMIŞ SORULAR VE ÇÖZÜMLERİ-5
| LGS'DE ÇIKAN SORU SAYISI | ||||
|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | |
| Soru Sayısı | 3 | 2 | 0 | 0 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 3 |
| 2018-2019 | 2 |
| 2019-2020 | 0 |
| 2020-2021 | 0 |
Aşağıda, 2013 yılından bu yana liselere giriş sınavlarında geometrik cisimlerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 3 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için önceki veya sonraki sayfaya geçebilirsiniz.
Şekildeki dik koninin taban çapının uzunluğu 24 cm ve |AC| = 18 cm'dir.
Buna göre bu koninin açınımı aşağıdakilerden hangisidir?
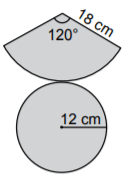
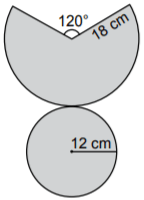
Çözüm:
Tabanı oluşturan dairenin yarıçapı r = 24 ÷ 2 = 12 cm ve yan yüzü oluşturan daire diliminin yarıçapı l = 18 cm'dir. Daire diliminin açısı ise ... ...'dir.
CEVAP: D
Bir üçgen dik prizmanın yan yüzlerinin alanları toplamı 108 cm2 dir.
Bu prizmanın yüksekliği 6 cm olduğuna göre tabanlarından biri aşağıdakilerden hangisi olabilir?
Çözüm:
Bir üçgen prizmanın yan yüzlerinin alanları toplamı, taban çevresi ile yüksekliğinin çarpımına eşittir. Buna göre, tabandaki üçgenin çevresi 108 ÷ 6 = 18 cm'dir. Çevresi 18 cm olan tek üçgen A seçeneğinde verilmiştir.
CEVAP: A
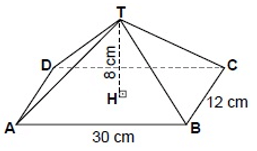
Şekildeki dikdörtgen dik piramidin yüksekliği 8 cm, |AB| = 30 cm ve |BC| = 12 cm'dir.
Buna göre bu piramidin yüzey alanı kaç santimetrekaredir?
Çözüm:
Bu piramidin yan yüzleri iki çeşit üçgenden oluşmaktadır. Bu üçgenlerden birinin tabanı 12 cm ve diğerinin tabanı 30 cm'dir. [AB]'nin orta noktasına F ve [BC]'nin orta noktasına E ismini verelim. Üçgenlerin yüksekliklerini bulabilmek için F ve E noktalarını T ve H noktaları ile birleştiren doğru parçaları çizelim.
Ön ve arka yüz
TFH dik üçgeninin hipotenüsü olan [TF] aynı zamanda TAB üçgeninin yüksekliğidir. |TH| = 8 cm ve |HF| = |BC| ÷ 2 = 12 ÷ 2 = 6 cm'dir. Pisagor teoremini kullanarak |TF| uzunluğunun 10 cm'ye eşit olduğu görebiliriz.
|TF|2 = |TH|2 + |HF|2
⇒ |TF|2 = 82 + 62 = 100 cm2
⇒ |TF| = 10 cm
Buna göre ön ve arka yüzlerin her birinin alanı (30 × 10) ÷ 2 = 150 cm2'dir.
Sol ve sağ yüz
Benzer şekilde, TBC üçgeninin yüksekliği olan [TE]'yi bulabilmek için Pisagor teoremini |TH| = 8 cm ve |HE| = 15 cm için kullanabiliriz.
|TE|2 = |TH|2 + |HE|2
⇒ |TE|2 = 82 + 152 = 289 cm2
⇒ |TE| = 17 cm
Buna göre sol ve sağ yüzlerin her birinin alanı (12 × 17) ÷ 2 = 102 cm2'dir.
Taban
Taban alanını 30 × 12 = 360 cm2'dir.
Toplam yüzey alanı
Toplam yüzey alanı
150 + 150 + 102 + 102 + 360 = 864 cm2'dir.
CEVAP: D
