BÖLÜM 6: DAİRE GRAFİĞİNİ SÜTUN VEYA ÇİZGİ GRAFİĞİNE DÖNÜŞTÜRME
Bu bölümde, daire dilimlerinin büyüklüklerinin ve/veya merkez açılarının verildiği farklı durumlarda, bir daire grafiğini çizgi veya sütun grafiğine nasıl dönüştürebileceğimizi öğreniyoruz.
A) BÜYÜKLÜKLERİN TAMAMI VERİLMİŞSE
Bir daire grafiğindeki tüm dilimlerin hangi büyüklüklere karşılık geldiğini bildiğimizi varsayalım. Bu grafiği
sütun veya çizgi grafiğine dönüştürebilmek için aşağıdaki adımları izleyebiliriz.
- Büyüklükleri gösteren bir dikey eksen ve bu büyüklüklerin hangi verilere ait olduğunu gösteren bir yatay eksen çizeriz.
- Sütun grafiğini oluştururken, parça büyüklükleri ile eşit uzunlukta sütunlar çizeriz.
- Çizgi grafiğini oluştururken, büyüklükleri gösteren noktaları grafikte işaretler, art arda gelen noktaları doğru parçaları ile birleştiririz.
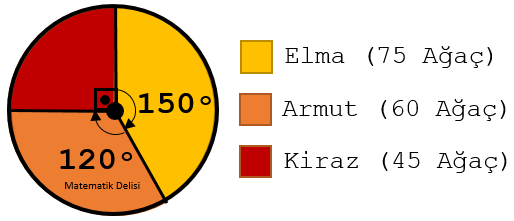
Bir meyve bahçesindeki farklı meyve ağaçlarının sayılarını gösteren yukarıdaki daire grafiğini sütun grafiğine dönüştürelim.
Yukarıdaki grafikte, hangi meyve ağacından kaç tane olduğu verilmiştir. Yapmamız gereken şey uygun eksenler seçip, verilen büyüklüklere göre sütunlar çizmektir.
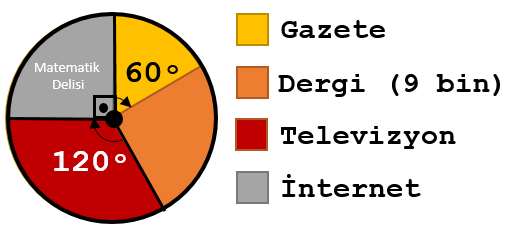
B) AÇILARIN TÜMÜ VE BÜYÜKLÜKLERİN BİR KISMI VERİLMİŞSE
Bir daire grafiğindeki açıların tamamını bildiğimiz halde, büyüklüklerin yalnız bir kısmı biliyorsak, aşağıdaki adımları
izleyerek sütun veya çizgi grafiklerini oluşturabiliriz.
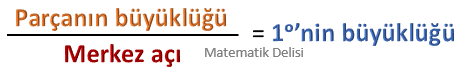
Bilinen büyüklüklerden birini bu büyüklüğün merkez açısına bölerek, 1°'lik açının hangi değere karşılık geldiğini buluruz.
- Parçaların merkez açılarını bulduğumuz değerle çarparak, büyüklüklerini hesaplarız.
- Bulduğumuz büyüklükleri çizgi veya sütun grafiğine yerleştiririz.
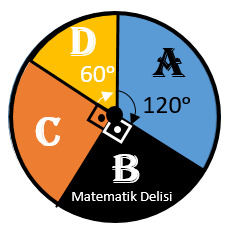
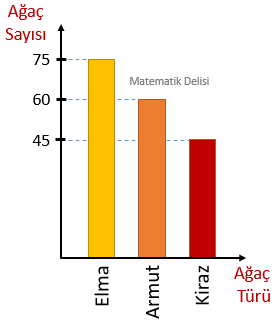
Yukarıdaki daire grafiği, 2019 yılında bir ilçede satılan A, B, C ve D marka otomobil sayıları kullanılarak oluşturulmuştur. Satılan D marka otomobil sayısı 30'dur. Bu bilgileri kullanarak satış rakamlarını gösteren bir sütun grafiği oluşturalım.
D marka otomobil, daire grafiğinde 60°'lik bir dilimle gösterilmiştir. 30 adet otomobil, 60° ile gösterildiğine göre, bu grafikteki her 1°'lik açı, 30 ÷ 60 = 0,5 otomobile karşılık gelmektedir.
Grafikteki diğer dilimlerin merkez açılarını 0,5 ile çarparak satılan otomobil sayılarını bulabiliriz.
A : 120 × 0,5 = 60 otomobil- B : 90 × 0,5 = 45 otomobil
C : 90 × 0,5 = 45 otomobilD : 30 otomobil
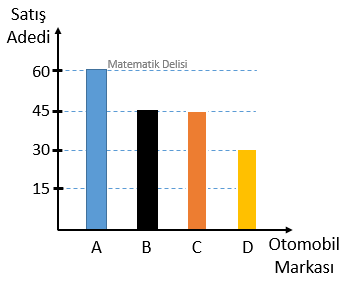
Uygun eksenler seçip, bulduğumuz büyüklükleri sütun grafiğine yerleştirerek aşağıdaki grafiği elde edebiliriz.
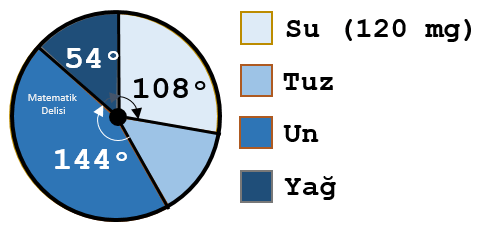
C) AÇILARDAN BİRİ VERİLMEMİŞSE
Bir daire grafiğindeki merkez açıların toplamı 360°'dir. Bu açılardan biri verilmemişse, verilmeyen açıyı bulabilmek için
360°'den diğer açıların toplamını çıkarırız.
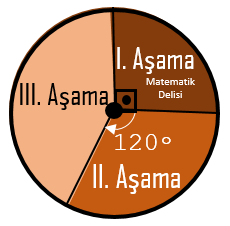
Yukarıdaki daire grafiği, 3 aşamadan oluşan bir yazılım projesinin her aşamasında kaç satır kod yazıldığını göstermektedir. Bu projenin 1. aşamasında 1800 satır kod yazılmıştır. Farklı aşamalardaki satır sayılarını çizgi grafiği ile gösterelim.
Daire grafiğinde III. aşamanın dışında kalan dilimlerin kaçar derece olduğu verilmiştir. III. aşamaya ait dilimin merkez açısını bulabilmek için 360°'den bu açıların toplamını çıkarabiliriz.
360° – (120° + 90°) = 150°
90° ile gösterilen I. aşamada yazılan satır sayısı 1800 olduğuna göre bu dairedeki 1°'lik açı, 1800 ÷ 90 = 20 satıra denk gelir. Merkez açıları 20 ile çarparak diğer aşamalarda kaçar satır kod yazıldığını bulabiliriz.
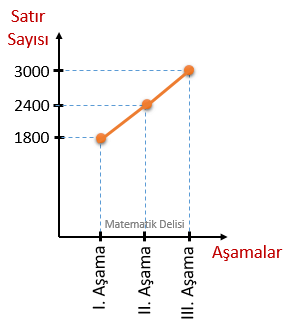
- II. Aşama: 120 × 20 = 2400 satır
- III. Aşama: 150 × 20 = 3000 satır
Bulduğumuz satır sayılarını çizgi grafiğine aşağıdaki gibi aktarabiliriz.
Aşağıdaki daire grafiklerini sütun grafiğine dönüştürün.
A)
B)
C)
D) BÜYÜKLÜKLERDEN HİÇBİRİ VERİLMEMİŞSE
Bir daire grafiğine ait hiçbir büyüklüğü bilmediğimiz durumda, merkez açıları kullanarak parçaların yüzdelerini
bulabilir ve bu yüzdelerle sütun veya çizgi grafiği oluşturabiliriz.
Merkez açıların toplamı 360° olduğu için bütünün % 1'i 3,6°'ye denk gelir. Bir daire diliminin merkez açısını 3,6°'ye bölerek, bu dilimle ifade edilen parçanın yüzde kaçlık bir bölüme karşılık geldiğini bulabiliriz.
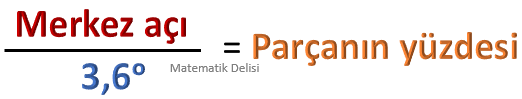
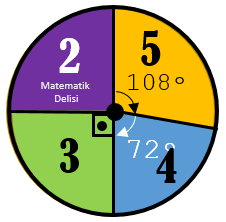
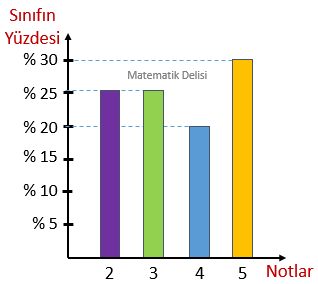
Bir sınıftaki öğrencilerin Matematik dersinden aldıkları notları gösteren daire grafiği yukarıda gösterilmiştir. Bu sınıfın yüzde kaçının hangi notu aldığını gösteren bir sütun grafiği oluşturalım.
Bu grafikte, ne sınıf mevcudu ne de hangi notu kaç kişinin aldığı bellidir. Bu nedenle, oluşturacağımız sütun grafiğinde büyüklükleri gösteremeyiz. Yalnız, merkez açıları 3,6°'ye bölerek dilimlerin yüzdelerini bulabiliriz.
2 alanların yüzdesi : 90 ÷ 3,6 = 253 alanların yüzdesi : 90 ÷ 3,6 = 254 alanların yüzdesi : 72 ÷ 3,6 = 205 alanların yüzdesi : 108 ÷ 3,6 = 30
Bulduğumuz yüzdeleri sütun grafiğinde aşağıdaki gibi gösterebiliriz.
