BÖLÜM 2: ONDALIK GÖSTERİMİ SAYI DOĞRUSUNDA GÖSTERME BÖLÜM 1

Sayı doğrusundaki her nokta bir sayıyı temsil eder. Yalnız doğal sayılar değil, ondalık gösterimle veya kesirle ifade edilen gerçek sayılar da sayı doğrusundaki noktalarla gösterilebilir.

Yukarıdaki sayı doğrusunda, 1 ve 2 doğal sayılarını görüyoruz. Bu sayıları gösteren noktalar arasında sonsuz tane daha nokta vardır. 1'den büyük ve 2'den küçük ondalık gösterimlerin tamamı, bu iki nokta arasında kalan doğru parçasının üzerindedir.

ÖRNEK:

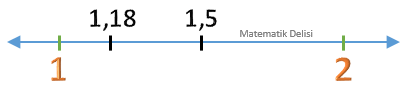
Sayı doğrusunda, 1,18 ve 1,5 gösterimlerini ifade eden noktalar, 1 ve 2 doğal sayılarının arasındadır.

Bir ondalık gösterim, tam kısımdaki doğal sayı ile bu doğal sayının bir fazlası arasındadır.

ÖRNEK:

3,1 sayısı 3 ile 4 arasındadır. Ondalık gösterimleri sıralamak için öğrendiğimiz kuralları uygularsak, 3,1’in 3’ten büyük ve 4’ten küçük olduğunu görebiliriz.

Ondalıklı Sayıları Sayı Doğrusunda Gösterme Örneği

3,1 sayısı 3 ile 4 arasında olduğuna göre, sayı doğrusunda da bu iki sayıyı gösteren noktaların arasında olmalıdır.

Alıştırmalar-4

Aşağıdaki ondalık gösterimlere en yakın tam sayıları bulun.

a) 15,678 : .... ile .... arasında

b) 431,4 : .... ile .... arasında

c) 0,18 : .... ile .... arasında

ç) 4,603 : .... ile .... arasında

d) 7,34 : .... ile .... arasında

e) 6,42 : .... ile .... arasında

Aşağıdaki örnekte, bir ondalık gösterimin sayı doğrusundaki yerini buluyoruz. Sonrasında ise, bu örnekteki çıkarımlarımızı kullanarak ondalık gösterimin sayı doğrusundaki yerini bulabilmek için daha genel, algoritmik bir yöntem öneriyoruz.

ÖRNEK:

3,1'in sayı doğrusundaki yerini bulalım.

Bu sayıyı tam ve ondalık kısımların toplamı şeklinde yazalım.

3,1 = 3 + 0,1

Bu toplamdaki 0,1 sayısı ... kesrine denk olduğu için 3,1 gösterimi, 3 ile ...'un toplamına eşittir. Buna göre 3,1 gösterimi sayı doğrusunda 3’ün ... birim sağındadır.

1 birimin 10 eşit parçaya bölünmesiyle elde edilen her bir parçanın uzunluğu, sayı doğrusunda ... birime denk gelir. Buna göre, 3 ile 4 arasındaki doğru parçası 10 eşit parçaya bölündüğünde, 3,1’in bulunduğu nokta 3’ün bir parça uzunluğu kadar sağında kalır.

Ondalıklı Sayıları Sayı Doğrusunda Gösterme

Sayı doğrusunda, bir parça uzunluğu kadar sağa gittikçe, her defasında sayının değeri 0,1 artar.

ONDALIK KISMI TEK BASAMAKLI OLAN SAYILAR

Ondalık kısmı tek basamaklı olan sayıları sayı doğrusunda gösterebilmek için,

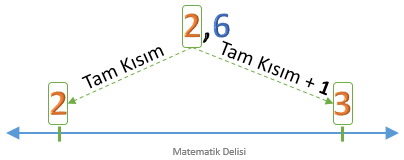
Bu sayının tam kısmındaki doğal sayıyı ve bu doğal sayının bir fazlasını buluruz.
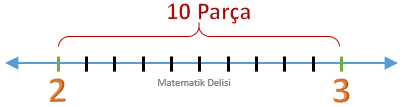
Sayı doğrusunun bu iki doğal sayının arasında kalan kısmını, 9 nokta ile 10 eşit parçaya ayırırız.
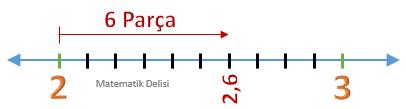
Tam kısımdaki doğal sayıyı gösteren noktadan, onda birler basamağındaki rakam kadar sağa ilerleriz.