SÜRE
40:002014-2015 TEOG 1. DÖNEM (MAZERET) MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2014-2015 TEOG 1. DÖNEM-MAZERET
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
2–2 sayısı aşağıdakilerden hangisine eşittir?
......
CEVAP: C
Aşağıdakilerin hangisinde verilen şekiller doğruya göre birbirinin ötelemeli yansımasıdır?
A seçeneğinde, doğrunun üstündeki şekli 3 birim sağa öteleyip, doğruya göre yansıttığımızda alttaki şekli elde ederiz. Bu nedenle, A seçeneğindeki şekiller birbirinin ötelemeli yansımasıdır.
CEVAP: A
... işleminin sonucu kaçtır?
1. Terim:
...............
2. Terim:
...............
Toplam:
0,9 + 1,2 = 2,1
CEVAP: D
Aşağıdakilerin hangisindeki sayıların çarpımı ... eder?
24 = 23 . 3 olduğundan
.........'dır.
... sayısı ise 2 ile ...'nın çarpımına eşittir.
CEVAP: A
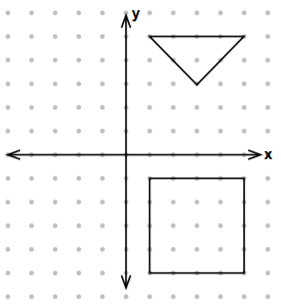
Şekildeki üçgen x eksenine göre yansıtıldığında kare ile birlikte oluşan şekil aşağıdakilerden hangisidir?
Üçgenin köşeleri (1, 5), (3, 3) ve (5, 5) koordinatlarındadır. Bu noktaların x-eksenine göre yansımaları sırasıyla (1, –5), (3, –3) ve (5, –5)'tir. Köşeleri bu noktalarda olan üçgen aşağıda sarı renkte gösterilmiştir.

CEVAP: B
36 . 3a = 912 olduğuna göre, a kaçtır?
Eşitliğin Solu:
Eşitliğin sol tarafındaki üslü ifadelerin tabanları aynı olduğu için kuvvetlerini toplarız.
36 . 3a = 36 + a
Eşitliğin Sağı:
Sağ taraftaki ifadenin tabanını 3 yapabilmek için 9 yerine 32 yazabiliriz.
912 = (32)12
Üslü sayının üssünü bulmak için kuvvetleri çarparız.
(32)12 = 32 × 12 = 324
Sol ve Sağ Tarafları Eşitleme:
Eşitliğin iki tarafındaki üslü sayıların tabanları eşit olduğu için kuvvetlerinin de eşit olması gerekir.
36 + a = 324
⇒ 6 + a = 24
⇒ a = 18
CEVAP: D
Babası Ali'ye ekim ayının yalnızca tam kare sayı olan günlerinde yirmişer lira harçlık vermiştir. Ali, ekim ayında toplam kaç lira harçlık almıştır?
Ekim ayı 31 gündür. Bu soruyu çözebilmek için 1'den 31'e kadar olan sayılardan kaçının tam kare olduğunu bulmamız gerekir. Belirtilen aralıktaki tam kare sayılar: 1, 4, 9, 16 ve 25'tir. Ekim ayında 5 tam kare sayı olduğu için Ali 5 defa harçlık almıştır. Her gün için 20 lira harçlık aldığına göre, babasının Ali'ye verdiği toplam para, 5 × 20 = 100 liradır.
CEVAP: C
... ve ... birer tamsayı olmak üzere, ... sayısı ... biçiminde yazılırsa ... toplamı aşağıdakilerden hangisi olabilir?
...... olduğu için
...'nin diğer ... biçimindeki yazılışları ve
... ve
... ve
... ve
CEVAP: B
Aşağıdakilerden hangisi ... ile bölündüğünde sonuç tam sayı olmaz?
A) ......... ↣
B) ......... ↣
C) ......... ↣
D) ......... ↣
CEVAP: A
...... işleminin sonucu kaçtır?
Mümkün olan tüm çarpanları kök dışına çıkaralım.
1. Terim:
......
2. Terim:
......
3. Terim:
......
Yeni bulduğumuz terimleri işlemde yerlerine yazarak sonuca ulaşabiliriz.
............
CEVAP: C
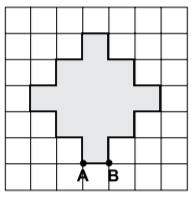
Kareli zeminde verilen yukarıdaki şeklin alanı 117 cm2 dir. Buna göre |AB| kaç santimetredir?
Verilen şekil 13 kareyi kaplamaktadır. Buna göre bir karenin alanı 117 ÷ 13 = 9 cm2'dir. Alanı 9 cm2 olan bir karenin kenar uzunluğu 3 cm'dir. |AB| uzunluğu, kareli zemindeki bir karenin kenar uzunluğuna eşit olduğu için cevap 3'tür.
CEVAP: B
... ile ... arasında kaç tam sayı vardır?
6'dan 10'a kadar olan tam sayılar (6, 7, 8, 9 ve 10), ... ile ... arasındadır.
CEVAP: B
......işleminin sonucu kaçtır?
Önce parantezlerden kurtulalım.
............
Tüm terimlerde karekök içerisindeki sayı aynı olduğu için katsayıları toplayalım. 3 + 1 – 1 + 2 = 5 olduğu için soruda verilen işlemin sonucu ...'dır.
CEVAP: D
... olduğuna göre, ... sayısı kaçtır?
63 = 32 . 7'dir. Bu nedenle ......'dir.
Buna göre a sayısı 3'e eşittir.
CEVAP: C

Yukarıdaki boyalı şeklin çevre uzunluğunun kaç milimetre olduğunu gösteren üslü ifade aşağıdakilerden hangisidir?
İki komşu nokta arasındaki mesafeye 1 birim dersek, şeklin çevresinin 16 birim olduğunu görebiliriz. Bir birim 8 mm'ye eşit olduğuna göre, şeklin çevresi 16 × 8 mm'dir. Tüm seçeneklerde tabanı 2 olan üslü ifadeler olduğu için yapmamız gereken şey 16 × 8'in 2 tabanındaki gösterimini bulmaktır.
8 = 23 ve 16 = 24 olduğu için çarpma sonucu
8 . 16 = 23 . 24 = 23 + 4 = 27'ye eşittir.
CEVAP: D
Bir bakteri kültüründeki bakteri sayısı, her gün bir önceki günün 10 katına çıkıyor.
Birinci günün sonunda kültürde 15 000 bakteri olduğuna göre, 4. günün sonundaki bakteri sayısının bilimsel gösterimi aşağıdakilerden hangisidir?
1.Yol:
Her gün için verilen sayıyı 10 ile çarparsak, 4. gün sonunda bu kültürde 15 000 000 bakteri olduğunu görebiliriz.
1'in sağında 7 rakam olduğu için, 15 000 000'un bilimsel gösterimi 1,5 × 107'dir.
2.Yol:
Bu soruyu çözmek için önce 15 000 sayısının bilimsel gösterimini bulup, her gün için 10'un kuvvetini 1 artırabiliriz. 15 000'in bilimsel gösterimi 1,5 × 104'tür. 1. ve 4. günler arasında 3 gün geçtiği için kuvveti 3 artırıp, sonucun 1,5 × 107'ye eşit olduğunu görebiliriz. C seçeneğindeki sayı doğru olduğu halde bilimsel gösterim değildir. Doğru cevap D seçeneğinde verilmiştir.
CEVAP: D
... olduğuna göre, ... kaçtır?
16 ve 625 sayıları aralarında asal olduğu için eşitliğin sağındaki kesirde herhangi bir sadeleşme olmaz.
0,4 sayısı ...'e eşittir. Eşitliğin sol tarafındaki 0,4 yerine ... yazdığımızda sol tarafta da bir kesir elde ederiz.
... ...
Elde ettiğimiz kesirde sadeleştirme olmayacağından, eşitliğin her iki tarafındaki kesirlerin pay ve paydalarını eşitleyebiliriz.
Buna göre, ... ve ... olmalıdır. ... olduğu için ... sayısı 4'e eşittir.
CEVAP: B
... sayısı aşağıdakilerden hangisine eşittir?
343'ü bölen listesi veya çarpan ağacı yöntemi ile çarpanlarına ayırabiliriz.
343 = 7 . 7 . 7 = 73
Buna göre, ... kesri, ...'e eşittir. İfadenin başındaki "–" işaretini de eklediğimizde sonucun –7–3 olduğunu görebiliriz.
CEVAP: A
1 kilogram unun tamamıyla aynı büyüklükte 4 ekmek yapılmaktadır. 128 kilogram unun tamamıyla aynı ekmeklerden kaç tane yapılır?
1 kilogram un ile 4 ekmek yapılabiliyorsa, 128 kilogram un ile 128 × 4 ekmek yapılabilir. 4 sayısı 22'ye eşittir. Ayrıca bölen listesi veya çarpan ağacı yöntemini kullanarak 128'in 27'ye eşit olduğunu görebiliriz.

Hem 4'ün hem de 128'in 2 tabanında üslü gösterimlerini bulduğumuza göre, bu sayıları çarpabiliriz.
128 . 4 = 27 . 22 = 27 + 2 = 29
CEVAP: D
Grafik: Sınavda Alınan Notlar

Bir sınavda alınan notlara göre öğrenci sayılarının dağılımına ait histogram yukarıda verilmiştir. 60'tan yüksek not alanların başarılı sayıldığı bu sınavda kaç öğrenci başarısız olmuştur?
Bu sınavda başarısız olan öğrencilerin sayısı histogramın en solundaki üç sütunun gösterdiği sayıların toplamına eşittir.
10 + 7 + 13 = 30
CEVAP: C