BÖLÜM 1: ÇARPAN AĞACI YÖNTEMİ İLE ASAL ÇARPANLARA AYIRMA
Bölen listesi yöntemine ek olarak,
bir sayıyı asal çarpanlarına ayırmanın diğer bir yolu da
çarpan ağacı oluşturmaktır. Çarpan ağacı, ters dönmüş bir ağaca benzer. Bu ağacın tepesinde
çarpanlara ayrılan sayı, dallarda ise bu sayının çarpanları bulunur.
Bu konuda sırasıyla,
- Çarpan ağacı oluşturarak bir sayıyı asal çarpanlarına nasıl ayırabileceğimizi ve
- Çarpan ağacını kullanarak bir sayının asal çarpanlarını nasıl bulabileceğimizi
öğreniyoruz.
ÇARPAN AĞACI İLE BİR SAYI ASAL ÇARPANLARINA NASIL AYRILIR?
Çarpan ağacı yönteminde,
Asal çarpanlarına ayıracağımız sayıyı yazar, bu sayıdan iki dal çıkarırız.
Çarpıldığında bu sayıya eşit olan 1'den büyük iki doğal sayı bulur, dalların ucuna bu doğal sayıları yazarız.
Yazdığımız doğal sayı
- asalsa daire içerisine alırız;
- asal değilse bu sayıdan iki dal çıkarır, önceki aşamada yaptığımız gibi çarpanları buluruz.
Tüm dalların ucundaki sayılar asal olana kadar, sayılardan dallar çıkarıp ağacı oluşturmaya devam ederiz.
- Son olarak, daire içerisindeki sayıları çarparız.
Şimdi de örnekleri inceleyelim.
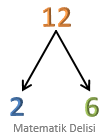
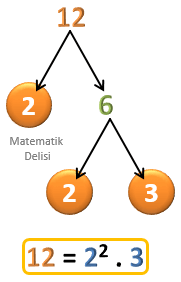
12'yi asal çarpanlarına ayıralım.
12 'yi ağacın tepesine yazdıktan sonra,12 'nin 1'den büyük hangi iki doğal sayının çarpımına eşit olduğunu buluyoruz.- Farklı tam sayı çiftleri bulabileceğimiz halde, bu örnekte
12 =2 ×6 çarpımını kullanıyoruz. 12 'den iki dal çıkarıp, dalların ucuna2 ve6 yazıyoruz.2 asal olduğu için daire içerisine alıp,6 ile devam ediyoruz.6 =2 ×3 olduğu için6 'dan iki dal çıkarıp uçlarına2 ve3 yazıyoruz.- Hem
2 hem de3 asal olduğu için bu sayıları da daire içerisine alıyoruz. 12 'nin asal çarpanlarına ayrılmış halini bulabilmek için dalların ucundaki tüm sayıları çarpıyoruz.12 =2 .2 .3 =2 2 .3
12'yi farklı bir ağacı kullanarak asal çarpanlarına ayıralım.
12 'yi yazdıktan sonra12 'nin 1'den büyük hangi iki doğal sayının çarpımına eşit olduğunu buluyoruz.- Önceki örnekte
12 =2 ×6 çarpımını kullanmıştık, bu defa12 =3 ×4 çarpımını kullanıyoruz. 12 'den iki dal çıkarıp,3 ve4 sayılarını dalların ucuna yazıyoruz.3 asal olduğu için daire içerisine alıp,4 ile devam ediyoruz.4 =2 ×2 olduğu için4 'ten iki dal çıkarıp uçlarına2 yazıyoruz.2 asal bir sayı olduğu için2 'leri de daire içerisine alıyoruz.12 'nin asal çarpanlarına ayrılmış halini bulabilmek için dalların ucundaki tüm sayıları çarpıyoruz.12 =3 .2 .2 =2 2 .3
15'i asal çarpanlarına ayıralım.
15 'i ağacın tepesine yazıp, bu sayının 1'den büyük hangi iki tam sayının çarpımına eşit olduğunu buluyoruz.15 =3 ×5 olduğu için15 'ten iki dal çıkarıp,3 ve5 sayılarını dalların ucuna yazıyoruz.3 ve5 asal olduğu için bu sayıları daire içerisine alıyoruz.15 'in asal çarpanlarına ayrılmış halini bulabilmek için daire içerisine aldığımız sayıları çarpıyoruz.15 =3 .5
60'ı asal çarpanlarına ayıralım.
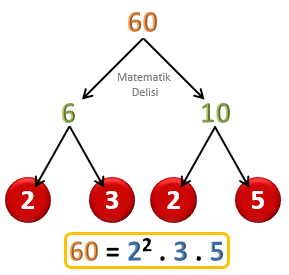
60 'ı çarpan ağacının tepesine yazdıktan sonra60 'ın 1'den büyük hangi iki tam sayının çarpımına eşit olduğunu buluyoruz.60 için birkaç farklı alternatif bulabiliriz ama bu örnekte60 =6 ×10 eşitliğini kullanıyoruz.60 'tan iki dal çıkarıp,6 ve10 sayılarını dalların ucuna yazıyoruz.- Ağacı oluşturmaya
6 ile devam ediyoruz. 6 =2 ×3 olduğu için6 'dan iki dal çıkarıp uçlarına2 ve3 yazıyoruz.2 ve3 asal olduğu için bu sayıları daire içerisine alıyoruz.- Ağaca
10 ile devam ediyoruz. 10 =2 ×5 olduğu için10 'dan iki dal çıkarıp uçlarına2 ve5 yazıyoruz.2 ve5 asal olduğu için bu sayıları daire içerisine alıyoruz.60 'ın asal çarpanlarına ayrılmış halini bulabilmek için daire içerisine aldığımız tüm sayıları çarpıyoruz.60 =2 .3 .2 .5 =2 2 .3 .5
60'ın farklı çarpan ağaçlarını görmek için tıklayın!
Çarpan ağacı yöntemini kullanarak aşağıdaki sayıları asal çarpanlarına ayırın.
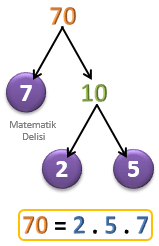
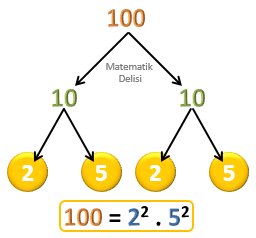
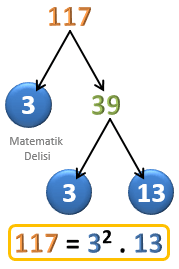
a) 32, b) 70, c) 100, d) 112, e) 117
Asal çarpanlara ayırmayla ilgili daha fazla alıştırma yapmak için bu bağlantıdaki listeyi kullanabilirsiniz.
Bulduğunuz sonuçların doğru olup olmadığını kontrol etmek için aşağıdaki hesaplama aracını da kullanabilirsiniz.
